# DAGs y Confusión {#sec-dags}
## Objetivos de aprendizaje
Al finalizar este capítulo, serás capaz de:
- Definir y construir Diagramas Acíclicos Dirigidos (DAGs)
- Distinguir entre causalidad y asociación
- Identificar confusores usando DAGs
- Aplicar las reglas de d-separación
## ¿Qué es un DAG?
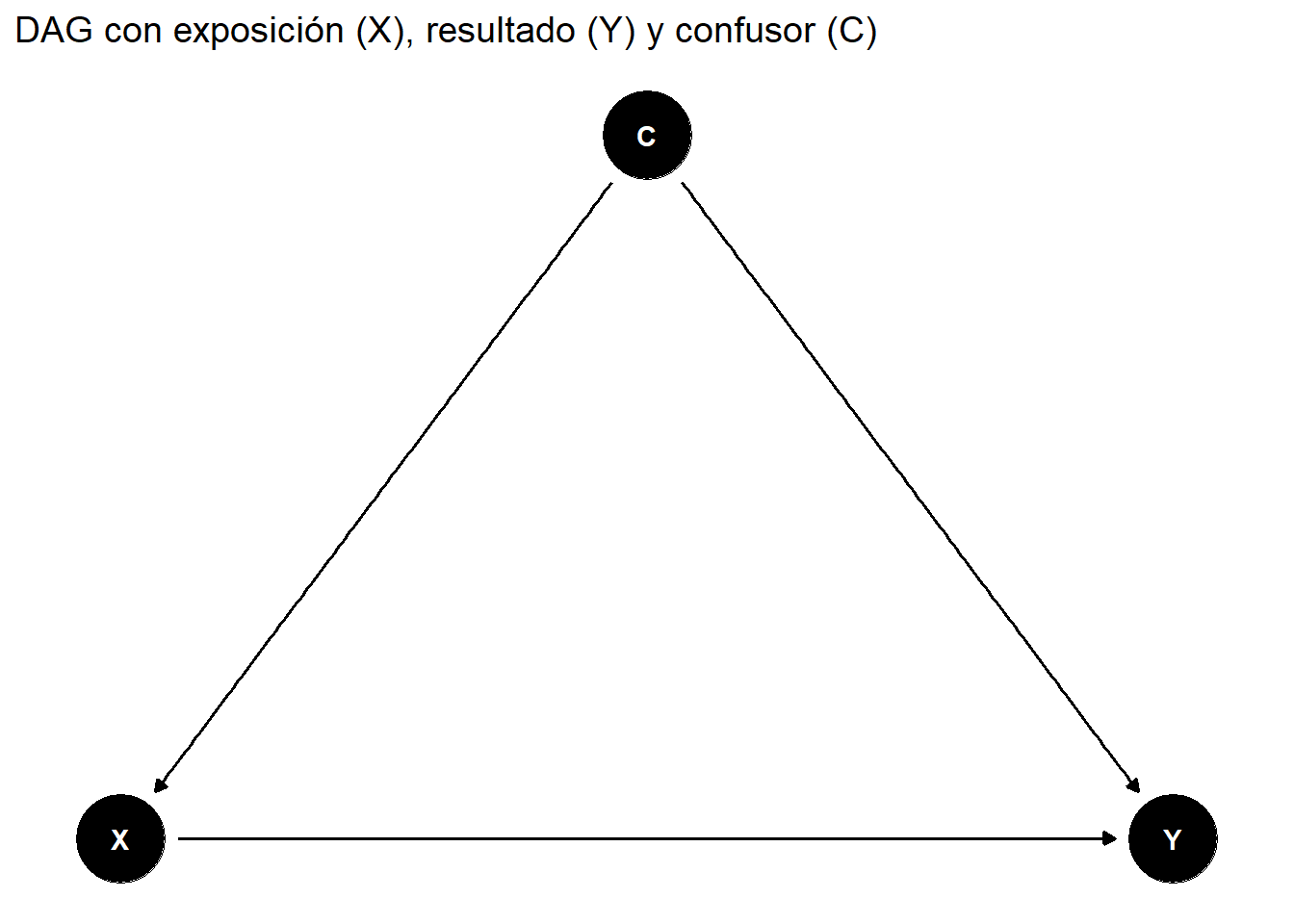
Un **Diagrama Acíclico Dirigido** (DAG, por sus siglas en inglés) es una representación gráfica de las relaciones causales entre variables.
::: {.callout-note}
## Definición
Un DAG es un grafo donde:
- **Dirigido**: Las flechas indican la dirección de la causalidad
- **Acíclico**: No hay ciclos (no puedes volver a una variable siguiendo las flechas)
:::
### Componentes de un DAG
```{r}
#| label: fig-dag-components
#| fig-cap: "Componentes básicos de un DAG"
#| code-fold: true
library(ggdag)
library(ggplot2)
# DAG simple
dag <- dagify(
Y ~ X + C,
X ~ C,
coords = list(
x = c(X = 0, Y = 2, C = 1),
y = c(X = 0, Y = 0, C = 1)
)
)
ggdag(dag) +
theme_dag() +
labs(title = "DAG con exposición (X), resultado (Y) y confusor (C)")
```
## Causalidad vs Asociación
### Asociación
Dos variables están **asociadas** si conocer el valor de una proporciona información sobre el valor de la otra.
$$P(Y|X) \neq P(Y)$$
### Causalidad
Una variable **causa** otra si intervenir sobre la primera cambia la distribución de la segunda.
$$P(Y|do(X)) \neq P(Y)$$
La notación $do(X)$ representa una intervención, no una observación.
## Tipos de caminos en un DAG
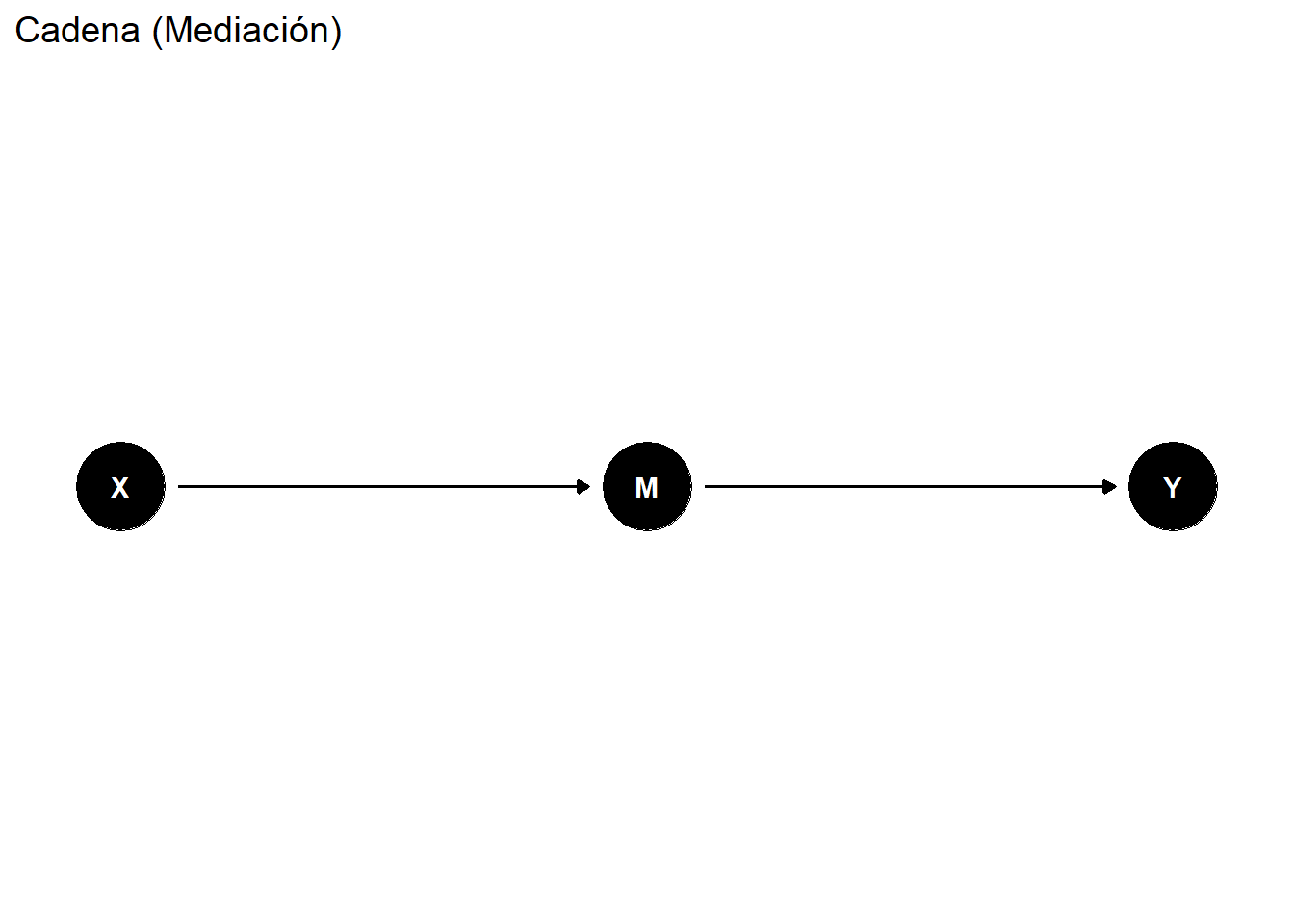
### Cadena (mediación)
```{r}
#| label: fig-chain
#| fig-cap: "Cadena: X → M → Y"
#| code-fold: true
chain <- dagify(
M ~ X,
Y ~ M,
coords = list(
x = c(X = 0, M = 1, Y = 2),
y = c(X = 0, M = 0, Y = 0)
)
)
ggdag(chain) +
theme_dag() +
labs(title = "Cadena (Mediación)")
```
En una cadena, X causa Y *a través de* M. Si controlamos por M, bloqueamos el efecto.
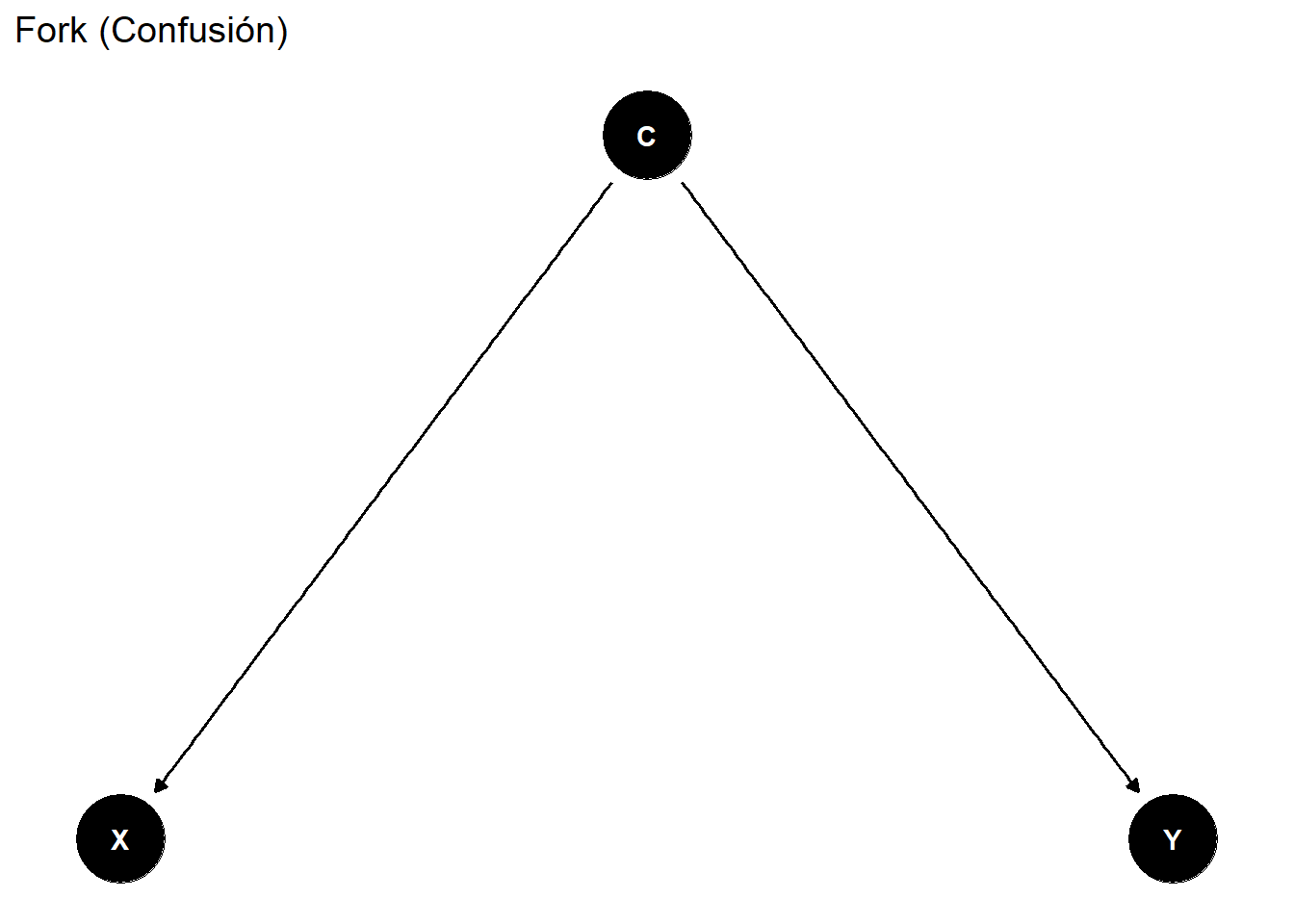
### Fork (confusión)
```{r}
#| label: fig-fork
#| fig-cap: "Fork: X ← C → Y"
#| code-fold: true
fork <- dagify(
X ~ C,
Y ~ C,
coords = list(
x = c(X = 0, C = 1, Y = 2),
y = c(X = 0, C = 1, Y = 0)
)
)
ggdag(fork) +
theme_dag() +
labs(title = "Fork (Confusión)")
```
En un fork, C es causa común de X e Y. X e Y están asociadas pero X no causa Y.
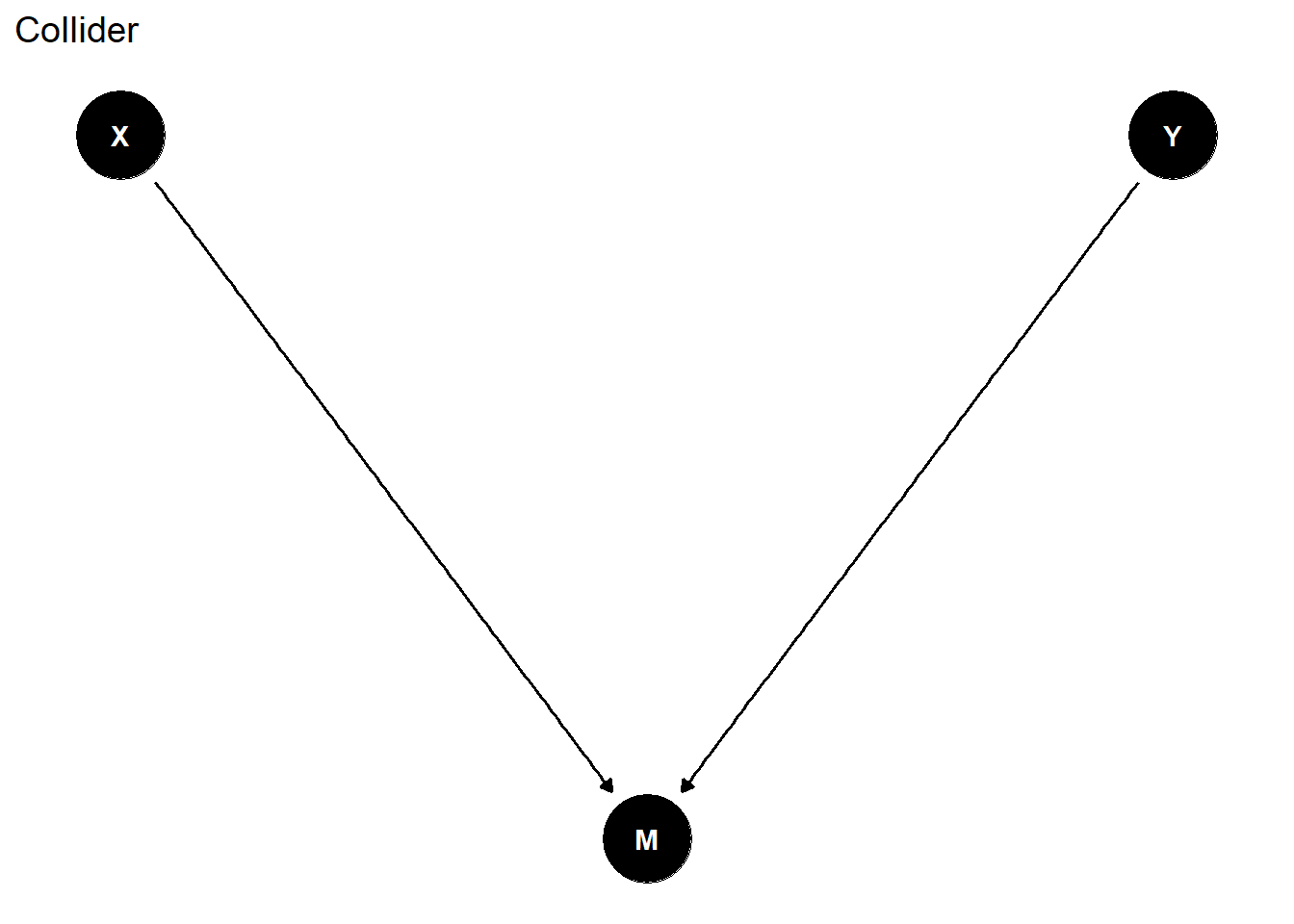
### Collider (colisionador)
```{r}
#| label: fig-collider
#| fig-cap: "Collider: X → M ← Y"
#| code-fold: true
collider <- dagify(
M ~ X + Y,
coords = list(
x = c(X = 0, M = 1, Y = 2),
y = c(X = 0, M = -0.5, Y = 0)
)
)
ggdag(collider) +
theme_dag() +
labs(title = "Collider")
```
En un collider, M es efecto de X e Y. X e Y no están asociadas, pero **se vuelven asociadas** si controlamos por M.
## D-separación
La **d-separación** es un criterio para determinar si dos variables son independientes dado un conjunto de variables condicionantes.
::: {.callout-important}
## Reglas de d-separación
1. **Cadenas y forks** están bloqueados si condicionamos en el nodo intermedio
2. **Colliders** están bloqueados por defecto, pero se abren si condicionamos en ellos (o sus descendientes)
:::
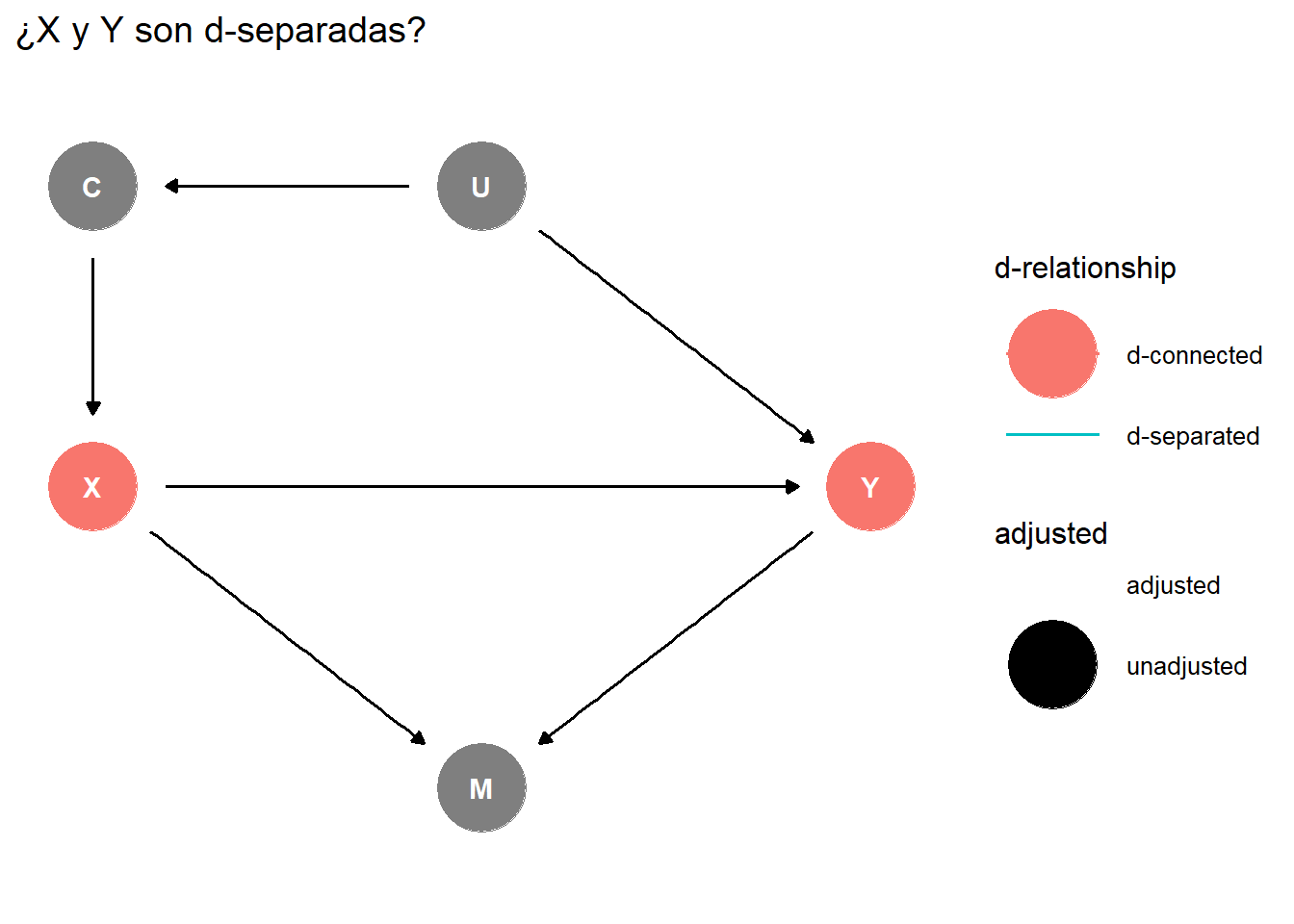
### Ejemplo
```{r}
#| label: fig-dsep-example
#| fig-cap: "Ejemplo de d-separación"
#| code-fold: true
example_dag <- dagify(
Y ~ X + U,
X ~ C,
C ~ U,
M ~ X + Y,
exposure = "X",
outcome = "Y",
coords = list(
x = c(X = 0, Y = 2, C = 0, U = 1, M = 1),
y = c(X = 0, Y = 0, C = 1, U = 1, M = -1)
)
)
ggdag_dseparated(example_dag, from = "X", to = "Y") +
theme_dag() +
labs(title = "¿X y Y son d-separadas?")
```
## Identificación de confusores
Un **confusor** es una variable que:
1. Causa (o está asociada con) la exposición
2. Causa (o está asociada con) el resultado
3. No está en el camino causal de X a Y
```{r}
#| label: fig-confounder-id
#| fig-cap: "Identificación de confusor usando dagitty"
#| code-fold: true
library(dagitty)
g <- dagitty("dag {
X -> Y
C -> X
C -> Y
}")
adjustmentSets(g, exposure = "X", outcome = "Y")
```
## Usando dagitty en R
El paquete `dagitty` permite:
1. Definir DAGs
2. Encontrar conjuntos de ajuste
3. Verificar d-separación
```{r}
#| label: dagitty-example
#| code-fold: false
library(dagitty)
# Definir DAG
mi_dag <- dagitty("dag {
Tratamiento -> Resultado
Edad -> Tratamiento
Edad -> Resultado
Sexo -> Resultado
}")
# Encontrar variables de ajuste
adjustmentSets(mi_dag,
exposure = "Tratamiento",
outcome = "Resultado")
```
## Aplicación: Ejemplo con datos
Consideremos un estudio sobre el efecto del ejercicio en la presión arterial:
```{r}
#| label: example-application
#| code-fold: false
# Simular datos
set.seed(42)
n <- 500
edad <- rnorm(n, 50, 10)
ejercicio <- 0.5 * edad + rnorm(n, 0, 5) # Edad afecta ejercicio
presion <- 100 + 0.5 * edad - 0.3 * ejercicio + rnorm(n, 0, 10)
datos <- data.frame(edad, ejercicio, presion)
# Sin ajustar por edad (sesgado)
modelo_crudo <- lm(presion ~ ejercicio, data = datos)
# Ajustando por edad
modelo_ajustado <- lm(presion ~ ejercicio + edad, data = datos)
# Comparar
cat("Efecto crudo:", round(coef(modelo_crudo)[2], 3), "\n")
cat("Efecto ajustado:", round(coef(modelo_ajustado)[2], 3), "\n")
```
## Ejercicios
::: {.callout-tip}
## Ejercicio 1
Construye un DAG para el siguiente escenario: Queremos estudiar el efecto del consumo de café en enfermedades cardíacas. Sabemos que el tabaquismo está asociado tanto con el consumo de café como con las enfermedades cardíacas.
:::
::: {.callout-tip}
## Ejercicio 2
Usando el paquete `dagitty`, determina el conjunto mínimo de variables que debes controlar para estimar el efecto causal.
:::
## Resumen
- Los DAGs son herramientas gráficas para representar asunciones causales
- Existen tres estructuras básicas: cadenas, forks y colliders
- La d-separación nos ayuda a identificar qué variables controlar
- Controlar por un collider introduce sesgo
- El paquete `dagitty` facilita el trabajo con DAGs en R
## Referencias {.unnumbered}