Al finalizar este capítulo, serás capaz de:
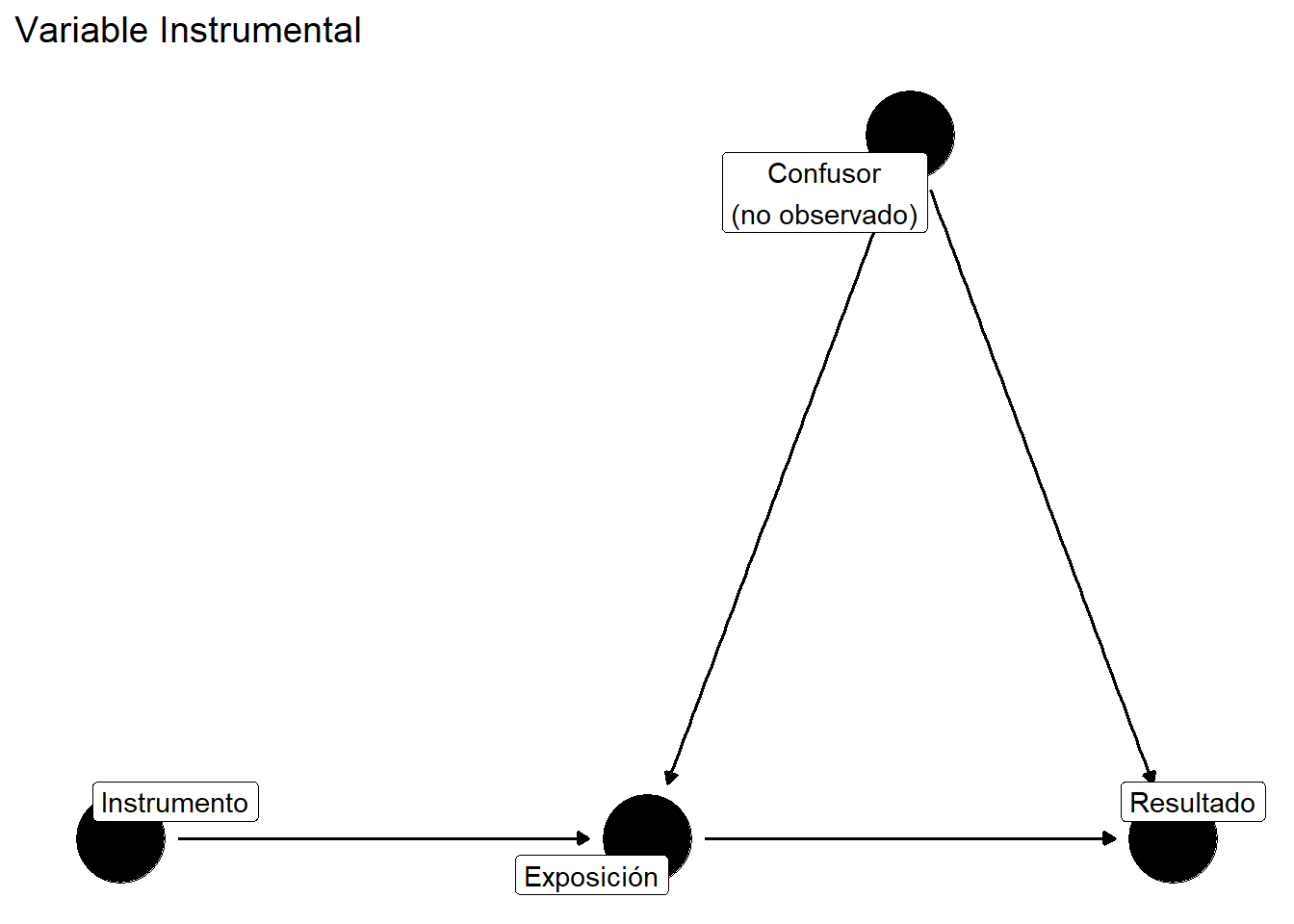
Una variable instrumental (IV) es una variable que afecta la exposición pero no tiene efecto directo sobre el resultado, excepto a través de la exposición.
library(ggdag)
library(ggplot2)
iv_dag <- dagify(
Y ~ X + U,
X ~ Z + U,
coords = list(
x = c(Z = 0, X = 1, Y = 2, U = 1.5),
y = c(Z = 0, X = 0, Y = 0, U = 1)
),
labels = c(
Z = "Instrumento",
X = "Exposición",
Y = "Resultado",
U = "Confusor\n(no observado)"
)
)
ggdag(iv_dag, text = FALSE, use_labels = "label") +
theme_dag() +
labs(title = "Variable Instrumental")
La condición de relevancia es la única verificable empíricamente.
# Simulación
set.seed(42)
n <- 5000
# Confusor no observado
U <- rnorm(n)
# Instrumento (ej: distancia a hospital)
Z <- rnorm(n)
# Exposición influenciada por Z y U
X <- 0.5 * Z + 0.8 * U + rnorm(n, 0, 0.5)
# Resultado influenciado por X y U
Y <- 2 * X + 1.5 * U + rnorm(n, 0, 1)
datos_iv <- data.frame(Z, X, Y, U)
# Primera etapa: Z -> X
primera_etapa <- lm(X ~ Z, data = datos_iv)
summary(primera_etapa)
Call:
lm(formula = X ~ Z, data = datos_iv)
Residuals:
Min 1Q Median 3Q Max
-3.1449 -0.6224 0.0190 0.6381 3.5124
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.01585 0.01331 -1.191 0.234
Z 0.50925 0.01321 38.549 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.941 on 4998 degrees of freedom
Multiple R-squared: 0.2292, Adjusted R-squared: 0.229
F-statistic: 1486 on 1 and 4998 DF, p-value: < 2.2e-16# Regla de oro: F > 10
cat("\nF-statistic:",
round(summary(primera_etapa)$fstatistic[1], 1), "\n")
F-statistic: 1486 El método de Mínimos Cuadrados en Dos Etapas (2SLS):
# Método manual (para entender)
# Etapa 1: Predecir X
etapa1 <- lm(X ~ Z, data = datos_iv)
datos_iv$X_pred <- predict(etapa1)
# Etapa 2: Usar X predicho
etapa2 <- lm(Y ~ X_pred, data = datos_iv)
cat("Efecto estimado por 2SLS:",
round(coef(etapa2)["X_pred"], 3), "\n")Efecto estimado por 2SLS: 1.994 cat("Efecto verdadero: 2\n")Efecto verdadero: 2library(ivreg)
# Estimación correcta con errores estándar apropiados
modelo_iv <- ivreg(Y ~ X | Z, data = datos_iv)
summary(modelo_iv)
Call:
ivreg(formula = Y ~ X | Z, data = datos_iv)
Residuals:
Min 1Q Median 3Q Max
-5.885405 -1.216900 -0.002617 1.223677 8.117727
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.01126 0.02559 -0.44 0.66
X 1.99359 0.04985 39.99 <2e-16 ***
Diagnostic tests:
df1 df2 statistic p-value
Weak instruments 1 4998 1486 <2e-16 ***
Wu-Hausman 1 4997 1148 <2e-16 ***
Sargan 0 NA NA NA
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.808 on 4998 degrees of freedom
Multiple R-Squared: 0.7412, Adjusted R-squared: 0.7411
Wald test: 1599 on 1 and 4998 DF, p-value: < 2.2e-16 # OLS (sesgado por confusión)
modelo_ols <- lm(Y ~ X, data = datos_iv)
cat("Efecto OLS (sesgado):", round(coef(modelo_ols)["X"], 3), "\n")Efecto OLS (sesgado): 3.042 cat("Efecto IV:", round(coef(modelo_iv)["X"], 3), "\n")Efecto IV: 1.994 cat("Efecto verdadero: 2\n")Efecto verdadero: 2El estimador IV identifica el Efecto Promedio del Tratamiento Local (LATE): el efecto entre los “compliers” (quienes cumplen con la asignación del instrumento).
tipos <- data.frame(
Tipo = c("Compliers", "Always-takers", "Never-takers", "Defiers"),
Z0_X = c("X=0", "X=1", "X=0", "X=1"),
Z1_X = c("X=1", "X=1", "X=0", "X=0"),
Descripcion = c(
"Tratados solo si Z=1",
"Siempre tratados",
"Nunca tratados",
"Tratados solo si Z=0"
)
)
knitr::kable(tipos,
col.names = c("Tipo", "Si Z=0", "Si Z=1", "Descripción"),
caption = "Tipos de individuos según respuesta al instrumento")| Tipo | Si Z=0 | Si Z=1 | Descripción |
|---|---|---|---|
| Compliers | X=0 | X=1 | Tratados solo si Z=1 |
| Always-takers | X=1 | X=1 | Siempre tratados |
| Never-takers | X=0 | X=0 | Nunca tratados |
| Defiers | X=1 | X=0 | Tratados solo si Z=0 |
Generalmente asumimos que no hay “defiers” (monotonía). Esto significa que el instrumento solo puede aumentar (o no cambiar) la probabilidad de tratamiento, nunca disminuirla.
| Contexto | Exposición | Instrumento |
|---|---|---|
| Retornos a educación | Años de educación | Trimestre de nacimiento |
| Efecto de cesárea | Tipo de parto | Preferencia del médico |
| Efecto de transfusión | Volumen transfundido | Distancia al banco de sangre |
| Randomización con incumplimiento | Tratamiento recibido | Asignación aleatoria |
Un instrumento débil tiene baja correlación con la exposición.
# Instrumento débil
set.seed(123)
Z_debil <- rnorm(n)
X_debil <- 0.05 * Z_debil + 0.8 * U + rnorm(n, 0, 0.5) # Coeficiente pequeño
Y_debil <- 2 * X_debil + 1.5 * U + rnorm(n, 0, 1)
# Primera etapa
etapa1_debil <- lm(X_debil ~ Z_debil)
cat("F-statistic (instrumento débil):",
round(summary(etapa1_debil)$fstatistic[1], 1), "\n")F-statistic (instrumento débil): 6.7 # IV con instrumento débil
datos_debil <- data.frame(Z = Z_debil, X = X_debil, Y = Y_debil)
modelo_iv_debil <- ivreg(Y ~ X | Z, data = datos_debil)
cat("Efecto IV (instrumento débil):",
round(coef(modelo_iv_debil)["X"], 3), "\n")Efecto IV (instrumento débil): 1.459 cat("Error estándar:",
round(summary(modelo_iv_debil)$coefficients["X", "Std. Error"], 3), "\n")Error estándar: 0.906 # Test de Cragg-Donald / Kleibergen-Paap
summary(modelo_iv, diagnostics = TRUE)
Call:
ivreg(formula = Y ~ X | Z, data = datos_iv)
Residuals:
Min 1Q Median 3Q Max
-5.885405 -1.216900 -0.002617 1.223677 8.117727
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.01126 0.02559 -0.44 0.66
X 1.99359 0.04985 39.99 <2e-16 ***
Diagnostic tests:
df1 df2 statistic p-value
Weak instruments 1 4998 1486 <2e-16 ***
Wu-Hausman 1 4997 1148 <2e-16 ***
Sargan 0 NA NA NA
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.808 on 4998 degrees of freedom
Multiple R-Squared: 0.7412, Adjusted R-squared: 0.7411
Wald test: 1599 on 1 and 4998 DF, p-value: < 2.2e-16 Cuando tienes más de un instrumento, puedes probar la validez del conjunto.
# Múltiples instrumentos
Z2 <- Z + rnorm(n, 0, 0.5) # Segundo instrumento
datos_iv$Z2 <- Z2
modelo_iv_multi <- ivreg(Y ~ X | Z + Z2, data = datos_iv)
summary(modelo_iv_multi, diagnostics = TRUE)
Call:
ivreg(formula = Y ~ X | Z + Z2, data = datos_iv)
Residuals:
Min 1Q Median 3Q Max
-5.885158 -1.216807 -0.002639 1.223392 8.117374
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.01126 0.02559 -0.44 0.66
X 1.99370 0.04984 40.00 <2e-16 ***
Diagnostic tests:
df1 df2 statistic p-value
Weak instruments 2 4997 743.291 <2e-16 ***
Wu-Hausman 1 4997 1148.871 <2e-16 ***
Sargan 1 NA 0.012 0.913
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.808 on 4998 degrees of freedom
Multiple R-Squared: 0.7412, Adjusted R-squared: 0.7412
Wald test: 1600 on 1 and 4998 DF, p-value: < 2.2e-16 Un economista quiere estimar el efecto de los años de educación sobre el salario. Propone usar la distancia al colegio más cercano como instrumento.
Simula un escenario donde el instrumento viola la restricción de exclusión (Z afecta Y directamente). ¿Qué sucede con la estimación IV?