# Causalidad y Supervivencia {#sec-survival}
## Objetivos de aprendizaje
Al finalizar este capítulo, serás capaz de:
- Integrar conceptos causales con análisis de supervivencia
- Reconocer los sesgos específicos de datos de tiempo al evento
- Aplicar métodos de ponderación para estimación causal
- Manejar riesgos competitivos desde una perspectiva causal
## Análisis de supervivencia: repaso
El **análisis de supervivencia** estudia el tiempo hasta que ocurre un evento de interés.
### Conceptos fundamentales
```{r}
#| label: survival-basics
#| code-fold: false
library(survival)
library(ggplot2)
# Datos de ejemplo
data(lung)
# Modelo de Kaplan-Meier
km_fit <- survfit(Surv(time, status) ~ sex, data = lung)
# Visualización
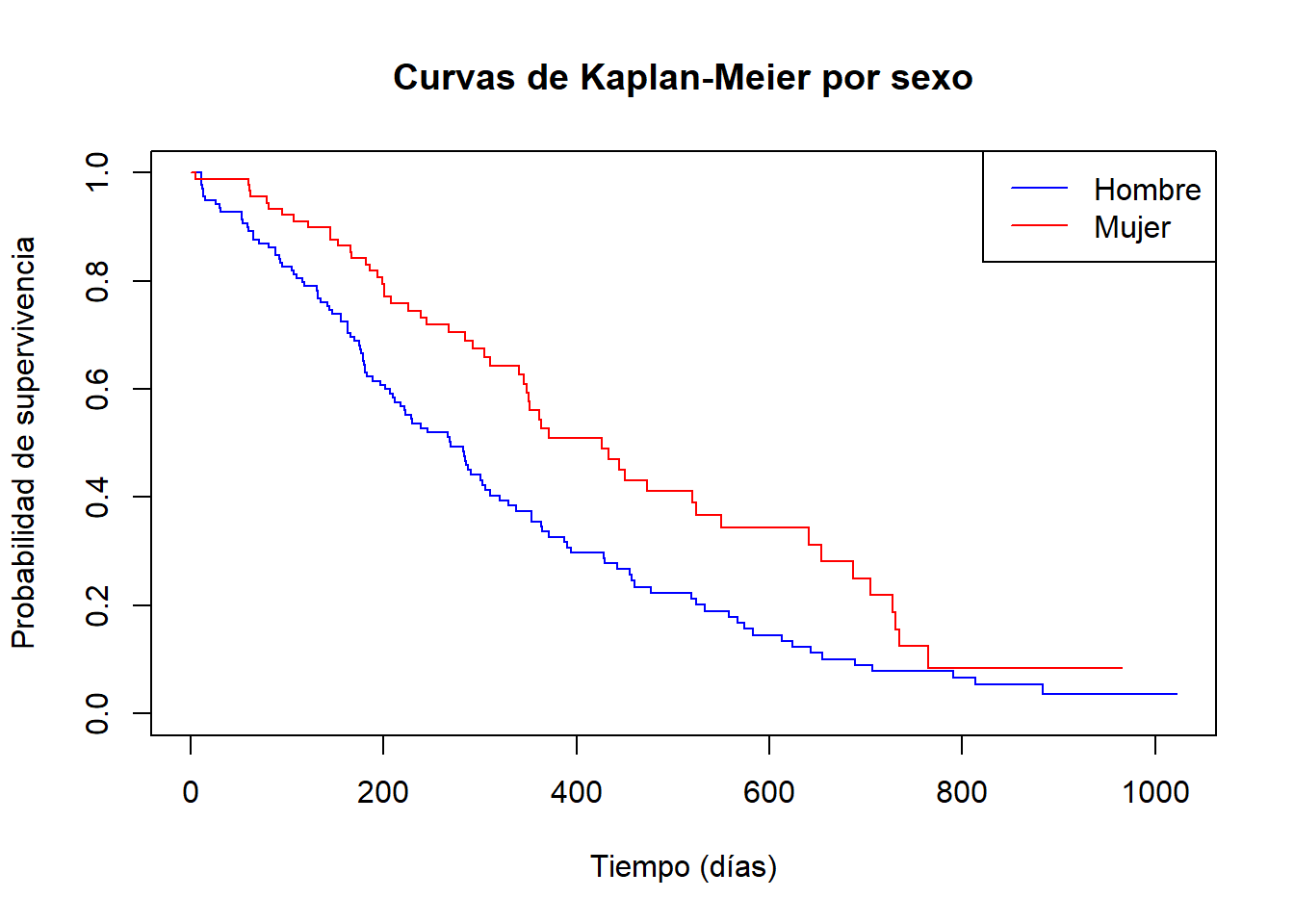
plot(km_fit, col = c("blue", "red"),
xlab = "Tiempo (días)",
ylab = "Probabilidad de supervivencia",
main = "Curvas de Kaplan-Meier por sexo")
legend("topright", c("Hombre", "Mujer"), col = c("blue", "red"), lty = 1)
```
## Sesgos en supervivencia
### Sesgo de tiempo inmortal
El **sesgo de tiempo inmortal** ocurre cuando hay un período durante el cual los sujetos expuestos no pueden experimentar el evento.
```{r}
#| label: fig-immortal-time
#| fig-cap: "Sesgo de tiempo inmortal"
#| code-fold: true
library(ggdag)
it_dag <- dagify(
Y ~ X + T,
X ~ T,
coords = list(
x = c(T = 0, X = 1, Y = 2),
y = c(T = 0, X = 0.3, Y = 0)
),
labels = c(
T = "Tiempo\n(sobrevivir\nhasta exposición)",
X = "Exposición",
Y = "Muerte"
)
)
ggdag(it_dag, text = FALSE, use_labels = "label") +
theme_dag() +
labs(title = "El tiempo de supervivencia necesario para exponerse crea sesgo")
```
### Ejemplo de sesgo de tiempo inmortal
```{r}
#| label: immortal-time-example
#| code-fold: false
# Simulación
set.seed(303)
n <- 1000
# Tiempo hasta exposición (si ocurre)
tiempo_exposicion <- rexp(n, 0.1)
# Tiempo de supervivencia verdadero (independiente de exposición)
tiempo_muerte_base <- rexp(n, 0.05)
# Asignación de exposición (solo si sobrevive hasta entonces)
datos_it <- data.frame(
id = 1:n,
tiempo_exposicion = tiempo_exposicion,
tiempo_muerte_base = tiempo_muerte_base
)
# ¿Se expuso? (solo si sobrevivió hasta el momento de exposición)
datos_it$expuesto <- datos_it$tiempo_muerte_base > datos_it$tiempo_exposicion
# Tiempo observado
datos_it$tiempo_observado <- pmin(datos_it$tiempo_muerte_base, 100)
datos_it$evento <- datos_it$tiempo_muerte_base <= 100
# Análisis INCORRECTO (ignora tiempo inmortal)
modelo_incorrecto <- coxph(Surv(tiempo_observado, evento) ~ expuesto,
data = datos_it)
cat("HR (análisis incorrecto, sesgo de tiempo inmortal):",
round(exp(coef(modelo_incorrecto)), 3), "\n")
cat("HR verdadero: 1.0 (la exposición no tiene efecto)\n")
```
### Corrección con tiempo dependiente
```{r}
#| label: time-varying-correction
#| code-fold: false
library(survival)
# Crear datos en formato largo (tiempo-dependiente)
datos_tv <- survSplit(Surv(tiempo_observado, evento) ~ .,
data = datos_it,
cut = datos_it$tiempo_exposicion[datos_it$expuesto],
episode = "periodo")
# Exposición como variable tiempo-dependiente
datos_tv$expuesto_tv <- with(datos_tv,
expuesto & tstart >= tiempo_exposicion)
# Análisis CORRECTO
modelo_correcto <- coxph(Surv(tstart, tiempo_observado, evento) ~ expuesto_tv,
data = datos_tv)
cat("HR (análisis correcto):",
round(exp(coef(modelo_correcto)), 3), "\n")
```
## Ponderación en supervivencia (IPTW)
Podemos combinar propensity scores con análisis de supervivencia.
```{r}
#| label: iptw-survival
#| code-fold: false
library(WeightIt)
# Datos con confusión
set.seed(404)
n <- 1500
datos_surv <- data.frame(
edad = rnorm(n, 60, 10),
comorbilidad = rbinom(n, 1, 0.3)
)
# Tratamiento influenciado por confusores
prob_trat <- plogis(-3 + 0.05 * datos_surv$edad + 1 * datos_surv$comorbilidad)
datos_surv$tratamiento <- rbinom(n, 1, prob_trat)
# Tiempo de supervivencia
hazard <- 0.01 * exp(0.03 * datos_surv$edad +
0.5 * datos_surv$comorbilidad -
0.4 * datos_surv$tratamiento) # Efecto protector
datos_surv$tiempo <- rexp(n, hazard)
datos_surv$tiempo <- pmin(datos_surv$tiempo, 100)
datos_surv$evento <- datos_surv$tiempo < 100
# Calcular pesos
pesos_surv <- weightit(tratamiento ~ edad + comorbilidad,
data = datos_surv,
method = "ps",
estimand = "ATE")
# Modelo sin ponderación (sesgado)
modelo_crudo <- coxph(Surv(tiempo, evento) ~ tratamiento,
data = datos_surv)
# Modelo ponderado
modelo_ponderado <- coxph(Surv(tiempo, evento) ~ tratamiento,
data = datos_surv,
weights = pesos_surv$weights,
robust = TRUE)
cat("HR crudo:", round(exp(coef(modelo_crudo)), 3), "\n")
cat("HR ponderado:", round(exp(coef(modelo_ponderado)), 3), "\n")
cat("HR verdadero: exp(-0.4) =", round(exp(-0.4), 3), "\n")
```
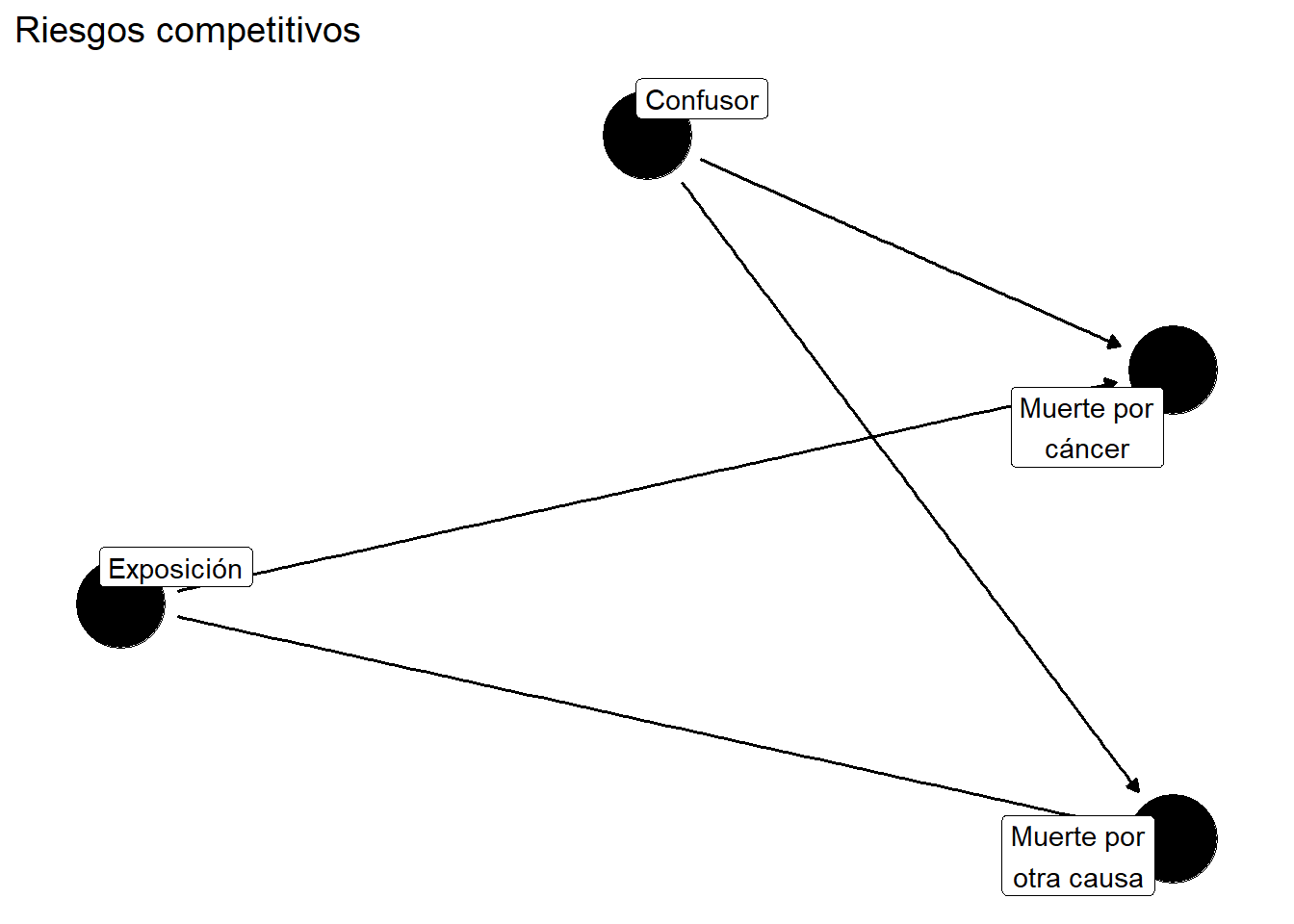
## Riesgos competitivos
Los **riesgos competitivos** ocurren cuando múltiples tipos de eventos pueden terminar el seguimiento.
```{r}
#| label: fig-competing-risks
#| fig-cap: "Estructura de riesgos competitivos"
#| code-fold: true
cr_dag <- dagify(
D1 ~ X + C,
D2 ~ X + C,
coords = list(
x = c(X = 0, C = 1, D1 = 2, D2 = 2),
y = c(X = 0, C = 1, D1 = 0.5, D2 = -0.5)
),
labels = c(
X = "Exposición",
C = "Confusor",
D1 = "Muerte por\ncáncer",
D2 = "Muerte por\notra causa"
)
)
ggdag(cr_dag, text = FALSE, use_labels = "label") +
theme_dag() +
labs(title = "Riesgos competitivos")
```
### Enfoque de subdistribución (Fine-Gray)
```{r}
#| label: fine-gray
#| code-fold: false
library(cmprsk)
# Simular riesgos competitivos
set.seed(505)
n <- 800
datos_cr <- data.frame(
tratamiento = rbinom(n, 1, 0.5)
)
# Dos tipos de eventos
tiempo_cancer <- rexp(n, 0.03 - 0.01 * datos_cr$tratamiento)
tiempo_otro <- rexp(n, 0.02)
# Evento observado
datos_cr$tiempo <- pmin(tiempo_cancer, tiempo_otro, 50)
datos_cr$tipo_evento <- ifelse(datos_cr$tiempo >= 50, 0,
ifelse(tiempo_cancer < tiempo_otro, 1, 2))
# Modelo Fine-Gray para muerte por cáncer
fg_fit <- crr(datos_cr$tiempo,
datos_cr$tipo_evento,
datos_cr[, "tratamiento", drop = FALSE],
failcode = 1)
summary(fg_fit)
```
### Interpretación causal
::: {.callout-warning}
## Cuidado con la interpretación
El modelo de Fine-Gray estima el efecto sobre la **incidencia acumulada**, no sobre el riesgo causa-específico. Esto tiene implicaciones para la interpretación causal porque incluye implícitamente los efectos sobre el riesgo competitivo.
:::
## Análisis causa-específico
```{r}
#| label: cause-specific
#| code-fold: false
# Análisis causa-específico (censurar el otro evento)
datos_cs <- datos_cr
datos_cs$evento_cancer <- as.numeric(datos_cs$tipo_evento == 1)
modelo_cs <- coxph(Surv(tiempo, evento_cancer) ~ tratamiento,
data = datos_cs)
cat("HR causa-específico (muerte por cáncer):",
round(exp(coef(modelo_cs)), 3), "\n")
```
## Ejercicios
::: {.callout-tip}
## Ejercicio 1
Un estudio encuentra que los pacientes que reciben un trasplante de riñón tienen mejor supervivencia que los que permanecen en diálisis. Sin embargo, los pacientes deben sobrevivir en lista de espera para recibir el trasplante.
1. Identifica el sesgo de tiempo inmortal
2. Propón un diseño analítico correcto
:::
::: {.callout-tip}
## Ejercicio 2
En un estudio de cáncer, algunos pacientes mueren por causas cardiovasculares antes de morir por cáncer.
1. ¿Cómo afecta esto la estimación del efecto del tratamiento?
2. Compara las estimaciones Fine-Gray vs causa-específica
:::
## Resumen
- El análisis de supervivencia requiere consideraciones causales especiales
- El sesgo de tiempo inmortal surge cuando la exposición requiere sobrevivir
- La solución es usar exposición como variable tiempo-dependiente
- IPTW se puede aplicar a modelos de supervivencia
- Los riesgos competitivos requieren elegir entre estimandos alternativos
- Fine-Gray vs causa-específico tienen diferentes interpretaciones causales
## Referencias {.unnumbered}