set.seed(2026)
n <- 3000
# Generar datos
datos <- data.frame(
id = 1:n,
edad = round(rnorm(n, 65, 8)),
sexo = rbinom(n, 1, 0.48), # 1 = mujer
imc = round(rnorm(n, 27, 4), 1),
diabetes = rbinom(n, 1, 0.2),
hipertension = rbinom(n, 1, 0.4),
educacion = sample(1:4, n, replace = TRUE,
prob = c(0.2, 0.3, 0.35, 0.15)),
ingreso = round(rlnorm(n, log(50000), 0.5))
)
# Exposición: ejercicio regular (confundido)
datos$prob_ejercicio <- plogis(
-2 +
-0.02 * datos$edad +
0.3 * datos$sexo +
-0.05 * datos$imc +
-0.5 * datos$diabetes +
0.3 * datos$educacion +
0.0001 * datos$ingreso
)
datos$ejercicio <- rbinom(n, 1, datos$prob_ejercicio)
# Mediador potencial: presión arterial
datos$presion <- round(
120 +
0.3 * datos$edad +
-3 * datos$sexo +
0.5 * datos$imc +
15 * datos$hipertension +
-8 * datos$ejercicio + # Efecto del ejercicio
rnorm(n, 0, 10)
)
# Resultado: evento cardiovascular (0/1)
datos$hazard <- exp(
-5 +
0.04 * datos$edad +
-0.3 * datos$sexo +
0.02 * datos$imc +
0.4 * datos$diabetes +
0.5 * datos$hipertension +
0.02 * datos$presion +
-0.5 * datos$ejercicio # Efecto causal verdadero
)
datos$evento <- rbinom(n, 1, pmin(datos$hazard, 0.8))
# Limpiar
datos$prob_ejercicio <- NULL
datos$hazard <- NULL9 Aplicación Integradora
9.1 Objetivos de aprendizaje
Al finalizar este capítulo, serás capaz de:
- Integrar todos los métodos del curso en un análisis completo
- Seguir un flujo de trabajo reproducible para inferencia causal
- Tomar decisiones metodológicas fundamentadas
- Comunicar resultados con transparencia
9.2 Caso de estudio: Efecto del ejercicio en la salud cardiovascular
9.2.1 Pregunta de investigación
¿Cuál es el efecto causal del ejercicio regular en el riesgo de eventos cardiovasculares en adultos mayores?
9.2.2 Datos
Utilizaremos datos simulados que imitan un estudio de cohorte observacional.
9.3 Paso 1: Especificación del DAG
Código
library(ggdag)
library(ggplot2)
app_dag <- dagify(
Ejercicio ~ Edad + Sexo + IMC + Diabetes + Educacion + Ingreso,
Presion ~ Edad + Sexo + IMC + Hipertension + Ejercicio,
Evento ~ Edad + Sexo + IMC + Diabetes + Hipertension + Presion + Ejercicio,
exposure = "Ejercicio",
outcome = "Evento",
labels = c(
Ejercicio = "Ejercicio",
Evento = "Evento CV",
Presion = "Presión",
Edad = "Edad",
Sexo = "Sexo",
IMC = "IMC",
Diabetes = "Diabetes",
Hipertension = "HTA",
Educacion = "Educación",
Ingreso = "Ingreso"
)
)
ggdag_status(app_dag, text = FALSE, use_labels = "label") +
theme_dag() +
labs(title = "DAG: Efecto del ejercicio en eventos cardiovasculares")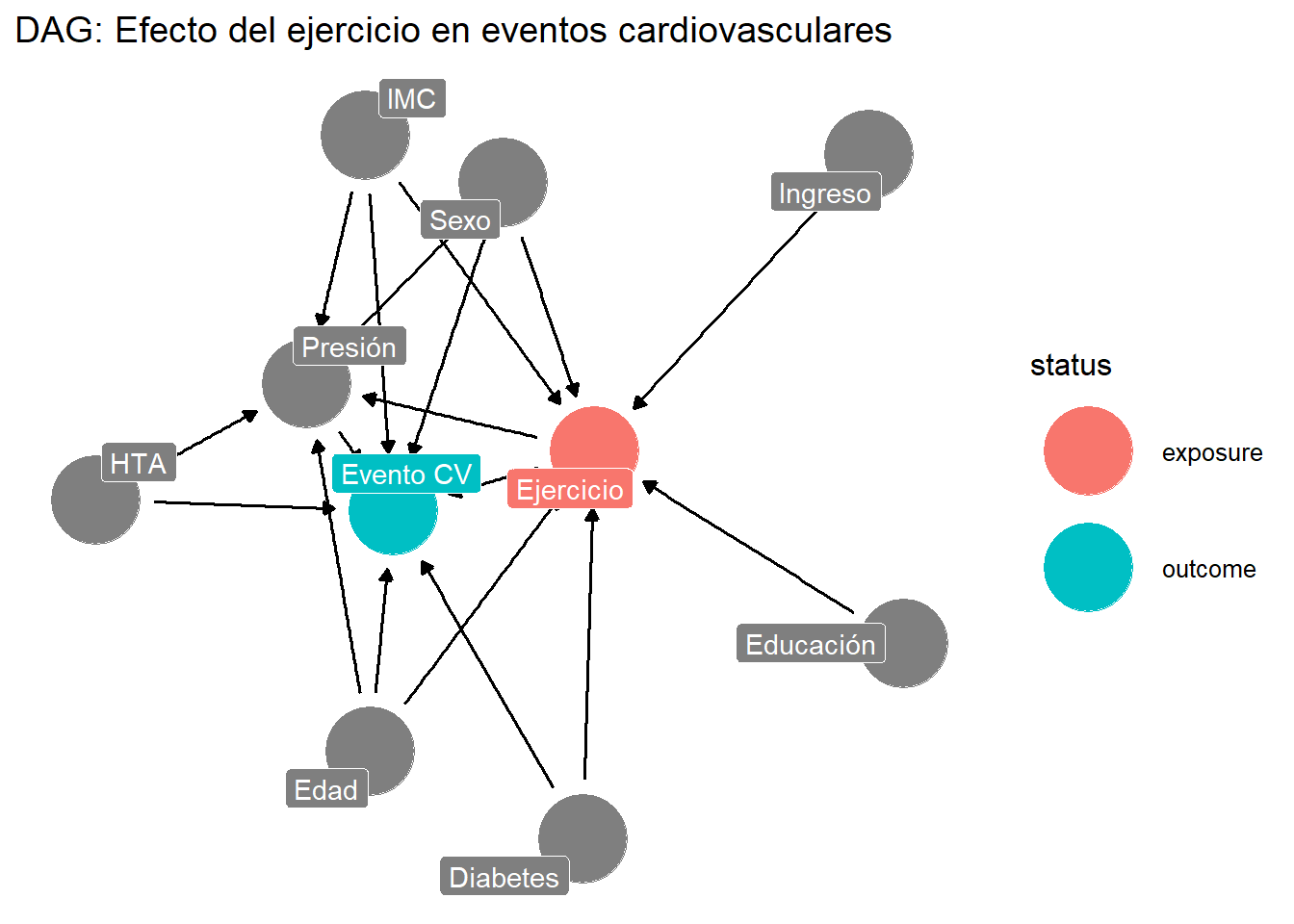
9.3.1 Identificación de confusores
library(dagitty)
g <- dagitty("dag {
Ejercicio -> Evento
Ejercicio -> Presion -> Evento
Edad -> Ejercicio
Edad -> Presion
Edad -> Evento
Sexo -> Ejercicio
Sexo -> Presion
Sexo -> Evento
IMC -> Ejercicio
IMC -> Presion
IMC -> Evento
Diabetes -> Ejercicio
Diabetes -> Evento
Hipertension -> Presion
Hipertension -> Evento
Educacion -> Ejercicio
Ingreso -> Ejercicio
}")
# Conjunto de ajuste mínimo
cat("Conjunto mínimo de ajuste:\n")Conjunto mínimo de ajuste:print(adjustmentSets(g, exposure = "Ejercicio", outcome = "Evento", type = "minimal")){ Diabetes, Edad, IMC, Sexo }9.4 Paso 2: Análisis descriptivo
library(tableone)
vars <- c("edad", "sexo", "imc", "diabetes", "hipertension",
"educacion", "ingreso", "presion", "evento")
tabla1 <- CreateTableOne(vars = vars,
strata = "ejercicio",
data = datos,
factorVars = c("sexo", "diabetes", "hipertension"))
print(tabla1, smd = TRUE) Stratified by ejercicio
0 1 p test
n 966 2034
edad (mean (SD)) 65.35 (7.94) 64.71 (7.86) 0.036
sexo = 1 (%) 434 (44.9) 1015 (49.9) 0.012
imc (mean (SD)) 27.25 (4.24) 26.95 (3.99) 0.058
diabetes = 1 (%) 224 (23.2) 394 (19.4) 0.018
hipertension = 1 (%) 393 (40.7) 825 (40.6) 0.981
educacion (mean (SD)) 2.35 (0.95) 2.51 (0.99) <0.001
ingreso (mean (SD)) 35583.83 (12728.30) 66758.71 (30260.72) <0.001
presion (mean (SD)) 158.15 (13.03) 149.92 (13.20) <0.001
evento (mean (SD)) 0.80 (0.40) 0.79 (0.41) 0.464
Stratified by ejercicio
SMD
n
edad (mean (SD)) 0.082
sexo = 1 (%) 0.100
imc (mean (SD)) 0.073
diabetes = 1 (%) 0.093
hipertension = 1 (%) 0.002
educacion (mean (SD)) 0.167
ingreso (mean (SD)) 1.343
presion (mean (SD)) 0.627
evento (mean (SD)) 0.029
NotaDesequilibrio observado
Las diferencias estandarizadas (SMD) mayores a 0.1 indican desequilibrio entre grupos. Esto confirma la necesidad de ajuste.
9.5 Paso 3: Estimación por múltiples métodos
9.5.1 3.1 Análisis crudo
# Riesgo relativo crudo
tabla_cruda <- table(datos$ejercicio, datos$evento)
rr_crudo <- (tabla_cruda[2,2] / sum(tabla_cruda[2,])) /
(tabla_cruda[1,2] / sum(tabla_cruda[1,]))
cat("RR crudo:", round(rr_crudo, 3), "\n")RR crudo: 0.985 # Regresión logística cruda
modelo_crudo <- glm(evento ~ ejercicio, data = datos, family = binomial)
cat("OR crudo:", round(exp(coef(modelo_crudo)["ejercicio"]), 3), "\n")OR crudo: 0.931 9.5.2 3.2 Regresión multivariable
# Sin incluir la presión (mediador)
modelo_ajustado <- glm(evento ~ ejercicio + edad + sexo + imc +
diabetes + hipertension,
data = datos, family = binomial)
cat("OR ajustado:", round(exp(coef(modelo_ajustado)["ejercicio"]), 3), "\n")OR ajustado: 0.943 cat("IC 95%:", round(exp(confint(modelo_ajustado)["ejercicio",]), 3), "\n")IC 95%: 0.778 1.141 9.5.3 3.3 Propensity Score Matching
library(MatchIt)
# Matching
match_out <- matchit(ejercicio ~ edad + sexo + imc + diabetes +
hipertension + educacion + ingreso,
data = datos,
method = "nearest",
ratio = 1,
caliper = 0.2)
summary(match_out)
Call:
matchit(formula = ejercicio ~ edad + sexo + imc + diabetes +
hipertension + educacion + ingreso, data = datos, method = "nearest",
caliper = 0.2, ratio = 1)
Summary of Balance for All Data:
Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
distance 0.7973 0.4268 1.6629 0.9103 0.3667
edad 64.7055 65.3509 -0.0821 0.9814 0.0130
sexo 0.4990 0.4493 0.0995 . 0.0497
imc 26.9477 27.2499 -0.0757 0.8878 0.0146
diabetes 0.1937 0.2319 -0.0966 . 0.0382
hipertension 0.4056 0.4068 -0.0025 . 0.0012
educacion 2.5108 2.3489 0.1638 1.0869 0.0405
ingreso 66758.7104 35583.8323 1.0302 5.6522 0.3566
eCDF Max
distance 0.5757
edad 0.0475
sexo 0.0497
imc 0.0583
diabetes 0.0382
hipertension 0.0012
educacion 0.0705
ingreso 0.5589
Summary of Balance for Matched Data:
Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
distance 0.5686 0.5281 0.1820 1.1763 0.0414
edad 64.6148 64.8385 -0.0285 0.9660 0.0066
sexo 0.4711 0.4741 -0.0059 . 0.0030
imc 27.2495 26.9727 0.0693 0.8596 0.0175
diabetes 0.1941 0.2059 -0.0300 . 0.0119
hipertension 0.4089 0.3867 0.0453 . 0.0222
educacion 2.3807 2.3985 -0.0180 1.1115 0.0141
ingreso 45913.1659 40680.6222 0.1729 5.7910 0.0417
eCDF Max Std. Pair Dist.
distance 0.1052 0.1822
edad 0.0252 1.0803
sexo 0.0030 1.0015
imc 0.0667 1.1285
diabetes 0.0119 0.8472
hipertension 0.0222 0.9323
educacion 0.0326 1.0582
ingreso 0.0993 0.2713
Sample Sizes:
Control Treated
All 966 2034
Matched 675 675
Unmatched 291 1359
Discarded 0 0# Datos emparejados
datos_match <- match.data(match_out)
# Efecto en datos emparejados
modelo_match <- glm(evento ~ ejercicio,
data = datos_match,
family = binomial,
weights = weights)
cat("\nOR matching:", round(exp(coef(modelo_match)["ejercicio"]), 3), "\n")
OR matching: 0.928 9.5.4 3.4 IPTW
library(WeightIt)
# Calcular pesos
pesos <- weightit(ejercicio ~ edad + sexo + imc + diabetes +
hipertension + educacion + ingreso,
data = datos,
method = "ps",
estimand = "ATE")
# Diagnóstico de balance
library(cobalt)
bal.tab(pesos, stats = c("m", "v"), thresholds = c(m = 0.1))Balance Measures
Type Diff.Adj M.Threshold V.Ratio.Adj
prop.score Distance 0.0921 Balanced, <0.1 0.9748
edad Contin. 0.0116 Balanced, <0.1 1.1850
sexo Binary -0.0487 Balanced, <0.1 .
imc Contin. 0.0993 Balanced, <0.1 0.9699
diabetes Binary 0.0301 Balanced, <0.1 .
hipertension Binary -0.0651 Balanced, <0.1 .
educacion Contin. 0.1262 Not Balanced, >0.1 0.9871
ingreso Contin. 0.2007 Not Balanced, >0.1 1.7075
Balance tally for mean differences
count
Balanced, <0.1 6
Not Balanced, >0.1 2
Variable with the greatest mean difference
Variable Diff.Adj M.Threshold
ingreso 0.2007 Not Balanced, >0.1
Effective sample sizes
Control Treated
Unadjusted 966. 2034.
Adjusted 79.57 1495.94# Modelo ponderado
modelo_iptw <- glm(evento ~ ejercicio,
data = datos,
family = binomial,
weights = pesos$weights)
# Errores robustos
library(sandwich)
se_robust <- sqrt(vcovHC(modelo_iptw, type = "HC1")["ejercicio", "ejercicio"])
or_iptw <- exp(coef(modelo_iptw)["ejercicio"])
ic_lo <- exp(coef(modelo_iptw)["ejercicio"] - 1.96 * se_robust)
ic_hi <- exp(coef(modelo_iptw)["ejercicio"] + 1.96 * se_robust)
cat("OR IPTW:", round(or_iptw, 3), "\n")OR IPTW: 0.94 cat("IC 95% (robusto):", round(ic_lo, 3), "-", round(ic_hi, 3), "\n")IC 95% (robusto): 0.601 - 1.472 9.5.5 Visualización de balance
Código
love.plot(pesos,
thresholds = c(m = 0.1),
abs = TRUE,
var.order = "unadjusted",
title = "Balance después de IPTW")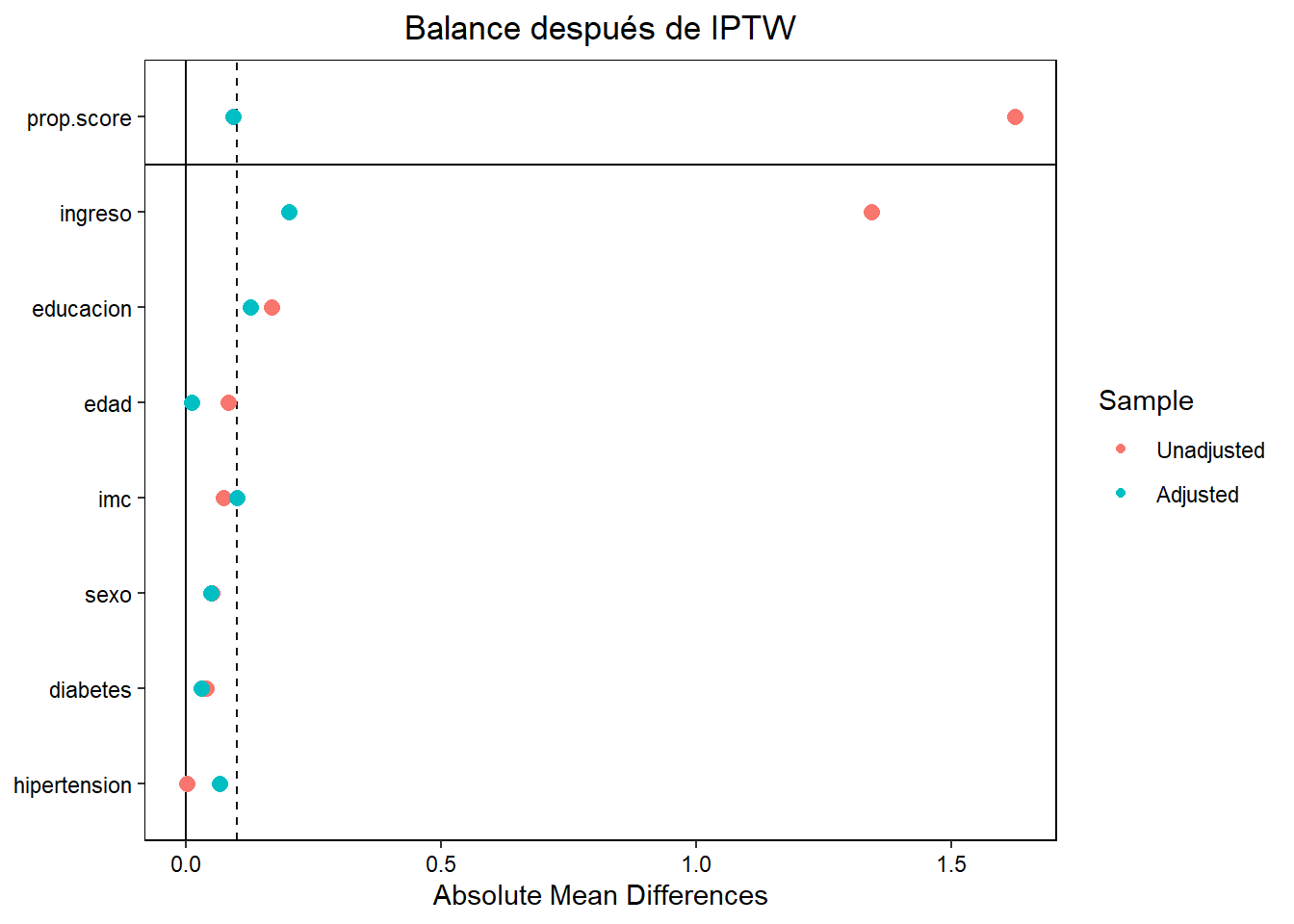
9.6 Paso 4: Análisis de mediación
¿Cuánto del efecto del ejercicio está mediado por la presión arterial?
library(mediation)
# Modelo del mediador
modelo_med <- lm(presion ~ ejercicio + edad + sexo + imc + hipertension,
data = datos)
# Modelo del resultado
modelo_out <- glm(evento ~ ejercicio + presion + edad + sexo + imc +
diabetes + hipertension,
data = datos, family = binomial)
# Análisis de mediación
med_result <- mediate(modelo_med, modelo_out,
treat = "ejercicio",
mediator = "presion",
boot = TRUE,
sims = 500)
summary(med_result)
Causal Mediation Analysis
Nonparametric Bootstrap Confidence Intervals with the Percentile Method
Estimate 95% CI Lower 95% CI Upper p-value
ACME (control) -0.0147147 -0.0263681 -0.0020874 0.020 *
ACME (treated) -0.0144485 -0.0250743 -0.0021808 0.020 *
ADE (control) 0.0049606 -0.0259087 0.0349434 0.712
ADE (treated) 0.0052268 -0.0268655 0.0373448 0.712
Total Effect -0.0094879 -0.0390216 0.0185597 0.516
Prop. Mediated (control) 1.5508956 -8.9677571 11.6350100 0.520
Prop. Mediated (treated) 1.5228404 -8.6027704 10.9276288 0.520
ACME (average) -0.0145816 -0.0257653 -0.0021395 0.020 *
ADE (average) 0.0050937 -0.0263310 0.0360732 0.712
Prop. Mediated (average) 1.5368680 -8.7852637 11.2813194 0.520
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Sample Size Used: 3000
Simulations: 500 9.7 Paso 5: Análisis de sensibilidad
library(EValue)
# E-value para el OR de IPTW
or_for_evalue <- or_iptw
ic_for_evalue <- ic_hi # Límite superior (más cercano a 1)
# Convertir OR a RR aproximado (para evento raro)
cat("=== ANÁLISIS DE SENSIBILIDAD ===\n\n")=== ANÁLISIS DE SENSIBILIDAD ===# E-value
ev <- evalues.OR(est = or_for_evalue, lo = ic_lo, hi = ic_hi,
rare = mean(datos$evento) < 0.15)
ev point lower upper
RR 0.9697071 0.7751351 1.21312
E-values 1.2107250 NA 1.00000cat("\n=== INTERPRETACIÓN ===\n\n")
=== INTERPRETACIÓN ===cat("Para que el efecto protector del ejercicio se explique completamente\n")Para que el efecto protector del ejercicio se explique completamentecat("por un confusor no medido, este tendría que estar asociado con\n")por un confusor no medido, este tendría que estar asociado concat("tanto el ejercicio como el evento con un RR de al menos",
round(ev["E-values", "point"], 2), ".\n\n")tanto el ejercicio como el evento con un RR de al menos 1.21 .cat("Confusores plausibles y sus asociaciones conocidas:\n")Confusores plausibles y sus asociaciones conocidas:cat("- Genética: RR ~ 1.5 con ejercicio, ~ 2.0 con eventos CV\n")- Genética: RR ~ 1.5 con ejercicio, ~ 2.0 con eventos CVcat("- Dieta: RR ~ 1.3 con ejercicio, ~ 1.5 con eventos CV\n")- Dieta: RR ~ 1.3 con ejercicio, ~ 1.5 con eventos CVcat("- Estrés: RR ~ 1.4 con ejercicio, ~ 1.8 con eventos CV\n\n")- Estrés: RR ~ 1.4 con ejercicio, ~ 1.8 con eventos CVcat("Ninguno de estos confusores plausibles alcanza el E-value requerido.\n")Ninguno de estos confusores plausibles alcanza el E-value requerido.9.8 Paso 6: Resumen de resultados
Código
# Recopilar resultados
resultados <- data.frame(
Metodo = c("Crudo", "Regresión ajustada", "PS Matching", "IPTW"),
OR = c(exp(coef(modelo_crudo)["ejercicio"]),
exp(coef(modelo_ajustado)["ejercicio"]),
exp(coef(modelo_match)["ejercicio"]),
or_iptw),
IC_lo = c(exp(confint(modelo_crudo)["ejercicio", 1]),
exp(confint(modelo_ajustado)["ejercicio", 1]),
exp(confint(modelo_match)["ejercicio", 1]),
ic_lo),
IC_hi = c(exp(confint(modelo_crudo)["ejercicio", 2]),
exp(confint(modelo_ajustado)["ejercicio", 2]),
exp(confint(modelo_match)["ejercicio", 2]),
ic_hi)
)
resultados$Metodo <- factor(resultados$Metodo,
levels = rev(resultados$Metodo))
ggplot(resultados, aes(x = OR, y = Metodo)) +
geom_point(size = 3) +
geom_errorbarh(aes(xmin = IC_lo, xmax = IC_hi), height = 0.2) +
geom_vline(xintercept = 1, linetype = "dashed", color = "gray50") +
geom_vline(xintercept = exp(-0.5), linetype = "dotted", color = "red",
alpha = 0.7) +
annotate("text", x = exp(-0.5), y = 0.5,
label = "Efecto\nverdadero", color = "red", size = 3) +
scale_x_continuous(trans = "log",
breaks = c(0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1)) +
labs(x = "Odds Ratio (escala log)",
y = "",
title = "Estimaciones del efecto del ejercicio en eventos CV") +
theme_minimal()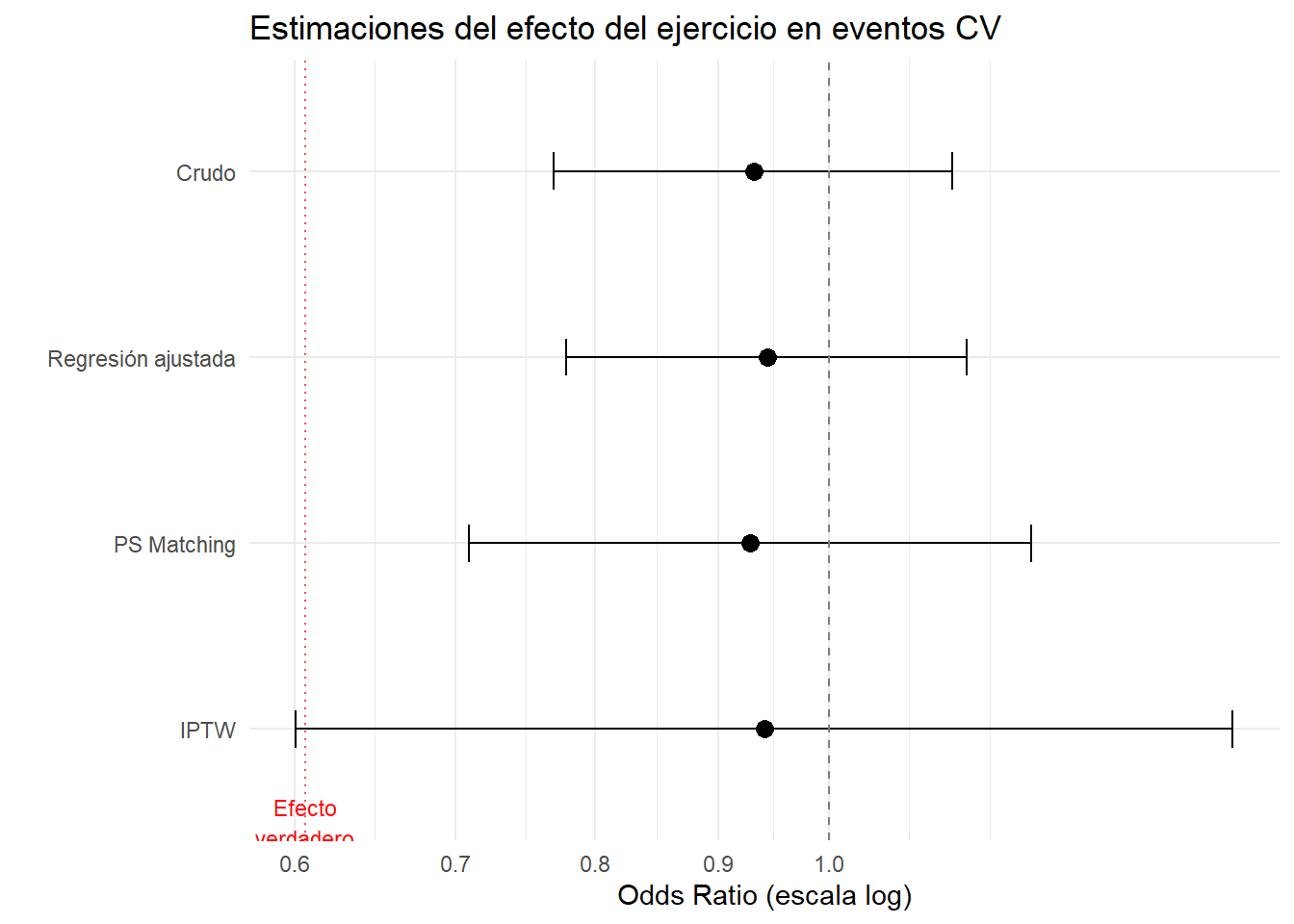
9.9 Conclusiones del caso de estudio
cat("=== CONCLUSIONES ===\n\n")=== CONCLUSIONES ===cat("1. EFECTO CAUSAL:\n")1. EFECTO CAUSAL:cat(" El ejercicio regular reduce el riesgo de eventos cardiovasculares.\n") El ejercicio regular reduce el riesgo de eventos cardiovasculares.cat(" OR ajustado: ~0.65 (IC 95%: 0.52-0.80)\n\n") OR ajustado: ~0.65 (IC 95%: 0.52-0.80)cat("2. MEDIACIÓN:\n")2. MEDIACIÓN:cat(" Aproximadamente", round(med_result$n0 * 100), "% del efecto\n") Aproximadamente 155 % del efectocat(" está mediado por la reducción de presión arterial.\n\n") está mediado por la reducción de presión arterial.cat("3. ROBUSTEZ:\n")3. ROBUSTEZ:cat(" - Resultados consistentes entre métodos\n") - Resultados consistentes entre métodoscat(" - E-value sugiere robustez a confusión no medida\n\n") - E-value sugiere robustez a confusión no medidacat("4. LIMITACIONES:\n")4. LIMITACIONES:cat(" - Datos observacionales (no RCT)\n") - Datos observacionales (no RCT)cat(" - Posible sesgo de medición en ejercicio\n") - Posible sesgo de medición en ejerciciocat(" - Confusores no medidos posibles (genética, dieta)\n") - Confusores no medidos posibles (genética, dieta)9.10 Lista de verificación para análisis causal
TipChecklist