# Análisis de Sensibilidad {#sec-sensitivity}
## Objetivos de aprendizaje
Al finalizar este capítulo, serás capaz de:
- Entender la importancia del análisis de sensibilidad
- Calcular e interpretar el E-value
- Aplicar métodos de sensibilidad cuantitativos
- Comunicar la robustez de hallazgos causales
## ¿Por qué análisis de sensibilidad?
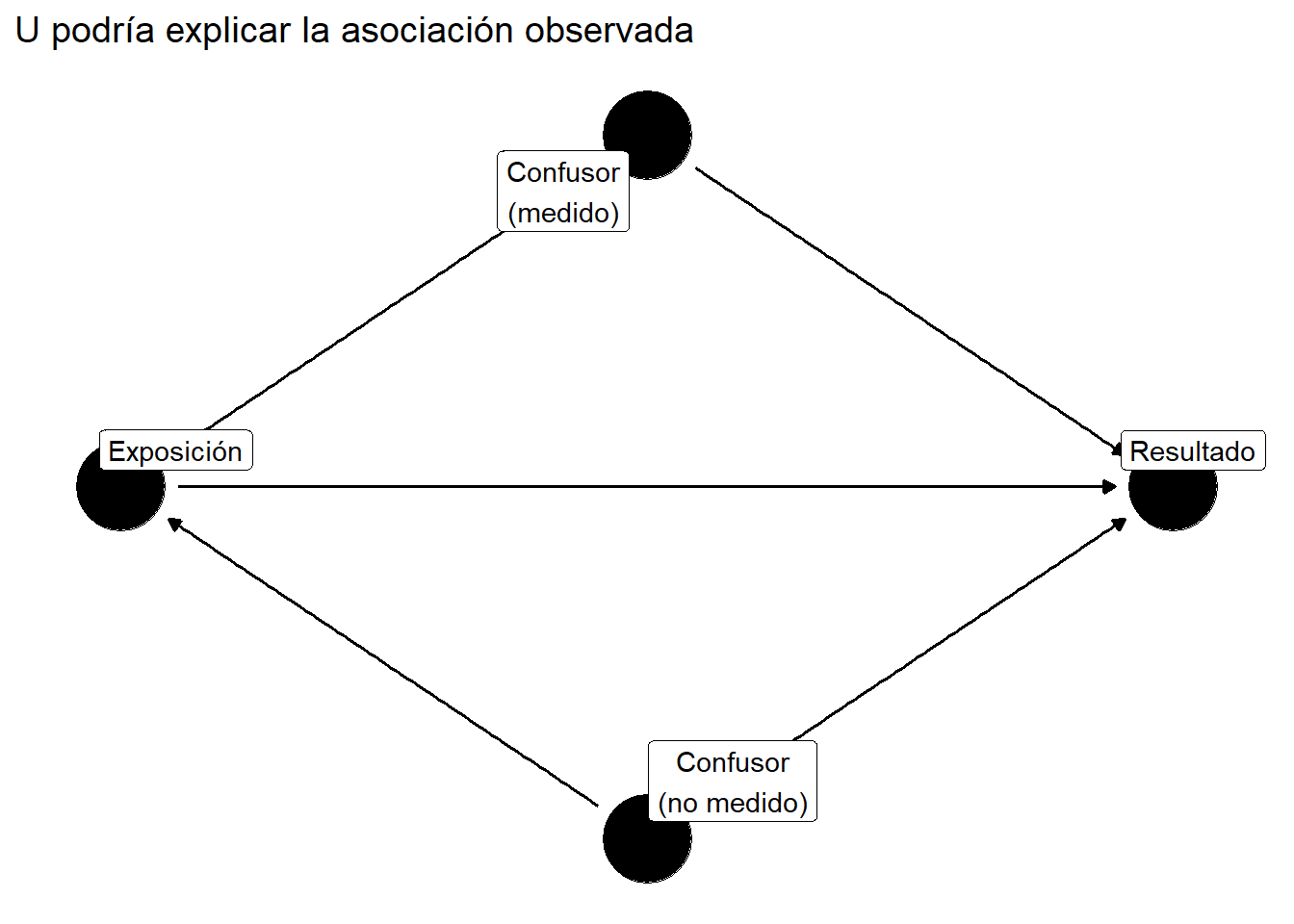
En estudios observacionales, **nunca podemos estar seguros** de haber controlado todos los confusores. El análisis de sensibilidad evalúa qué tan fuertes tendrían que ser los confusores no medidos para explicar nuestros resultados.
```{r}
#| label: fig-unmeasured-conf
#| fig-cap: "El confusor no medido (U) amenaza la validez"
#| code-fold: true
library(ggdag)
library(ggplot2)
sens_dag <- dagify(
Y ~ X + C + U,
X ~ C + U,
coords = list(
x = c(X = 0, Y = 2, C = 1, U = 1),
y = c(X = 0, Y = 0, C = 0.7, U = -0.7)
),
labels = c(
X = "Exposición",
Y = "Resultado",
C = "Confusor\n(medido)",
U = "Confusor\n(no medido)"
)
)
ggdag(sens_dag, text = FALSE, use_labels = "label") +
theme_dag() +
labs(title = "U podría explicar la asociación observada")
```
## El E-value
El **E-value** [@vanderweele2019evalue] es la asociación mínima que un confusor no medido tendría que tener con *tanto* la exposición *como* el resultado para explicar completamente la asociación observada.
$$E\text{-value} = RR + \sqrt{RR \times (RR - 1)}$$
```{r}
#| label: evalue-calculation
#| code-fold: false
library(EValue)
# Ejemplo: RR observado = 2.5
rr_observado <- 2.5
ic_inferior <- 1.8 # Límite inferior del IC 95%
# Calcular E-value
evalues <- evalues.RR(est = rr_observado, lo = ic_inferior)
evalues
```
### Interpretación del E-value
```{r}
#| label: fig-evalue-interpretation
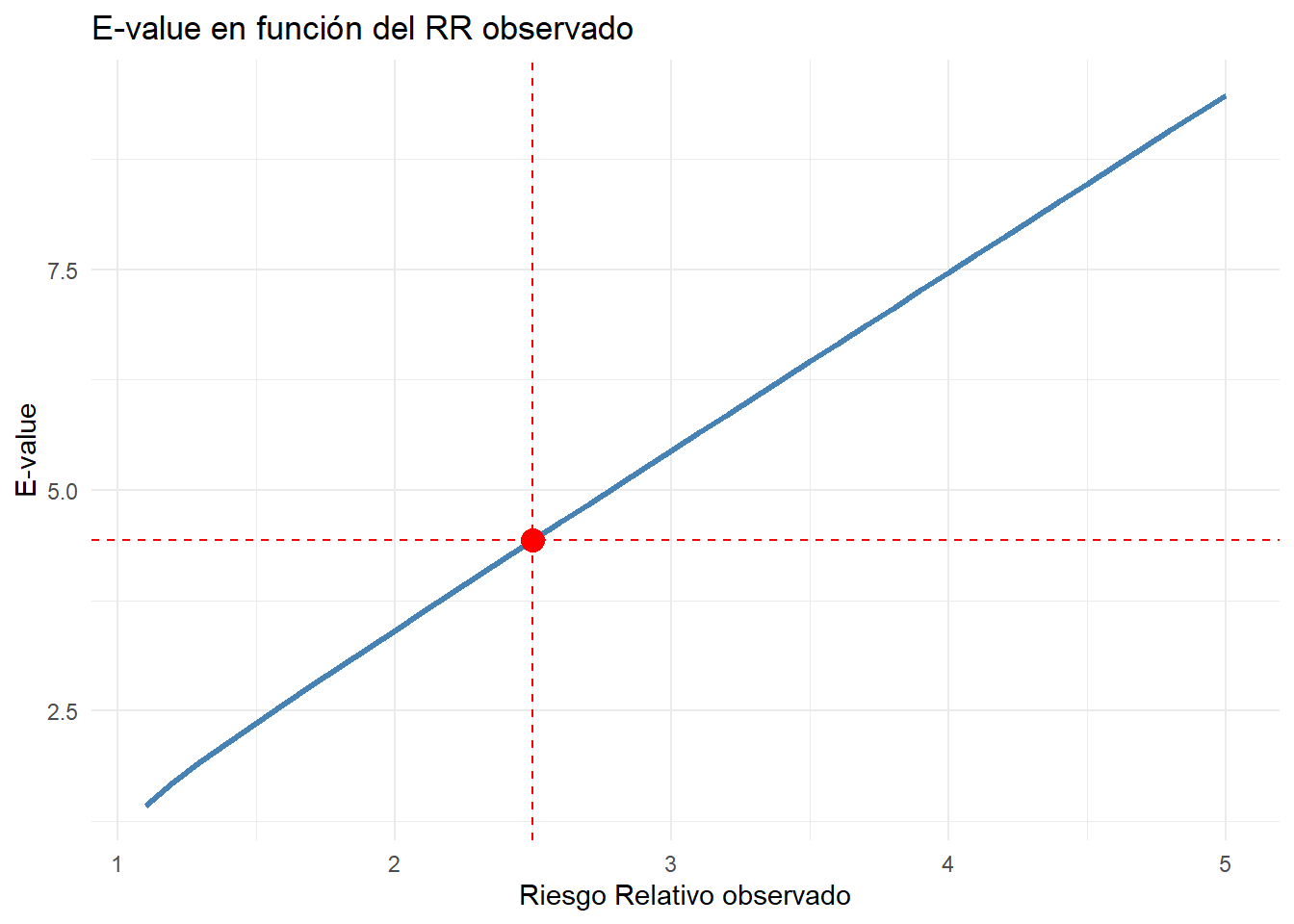
#| fig-cap: "Interpretación gráfica del E-value"
#| code-fold: true
# Crear datos para el gráfico
rr_seq <- seq(1.1, 5, 0.1)
evalue_seq <- rr_seq + sqrt(rr_seq * (rr_seq - 1))
plot_data <- data.frame(
RR = rr_seq,
EValue = evalue_seq
)
# Valores del ejemplo anterior
rr_ejemplo <- 2.5
evalue_ejemplo <- 2.5 + sqrt(2.5 * (2.5 - 1))
ggplot(plot_data, aes(x = RR, y = EValue)) +
geom_line(size = 1.2, color = "steelblue") +
geom_vline(xintercept = rr_ejemplo, linetype = "dashed", color = "red") +
geom_hline(yintercept = evalue_ejemplo, linetype = "dashed", color = "red") +
annotate("point", x = rr_ejemplo, y = evalue_ejemplo, size = 4, color = "red") +
labs(x = "Riesgo Relativo observado",
y = "E-value",
title = "E-value en función del RR observado") +
theme_minimal()
```
::: {.callout-note}
## Interpretación
Para un RR de 2.5, el E-value es aproximadamente 4.4. Esto significa que un confusor no medido tendría que tener un RR de al menos 4.4 con tanto la exposición como el resultado para explicar completamente la asociación observada.
:::
## Análisis de sensibilidad con sensemakr
El paquete `sensemakr` [@cinelli2020making] proporciona herramientas más sofisticadas.
```{r}
#| label: sensemakr-example
#| code-fold: false
library(sensemakr)
# Ejemplo con datos de discriminación laboral
data("darfur")
# Modelo ajustado
modelo <- lm(peacefactor ~ directlyharmed + age + farmer_dar +
herder_dar + pastvoted + female, data = darfur)
# Análisis de sensibilidad
sens <- sensemakr(model = modelo,
treatment = "directlyharmed",
benchmark_covariates = "female",
kd = 1:3,
q = 1)
summary(sens)
```
### Visualización de contornos
```{r}
#| label: fig-contour-plot
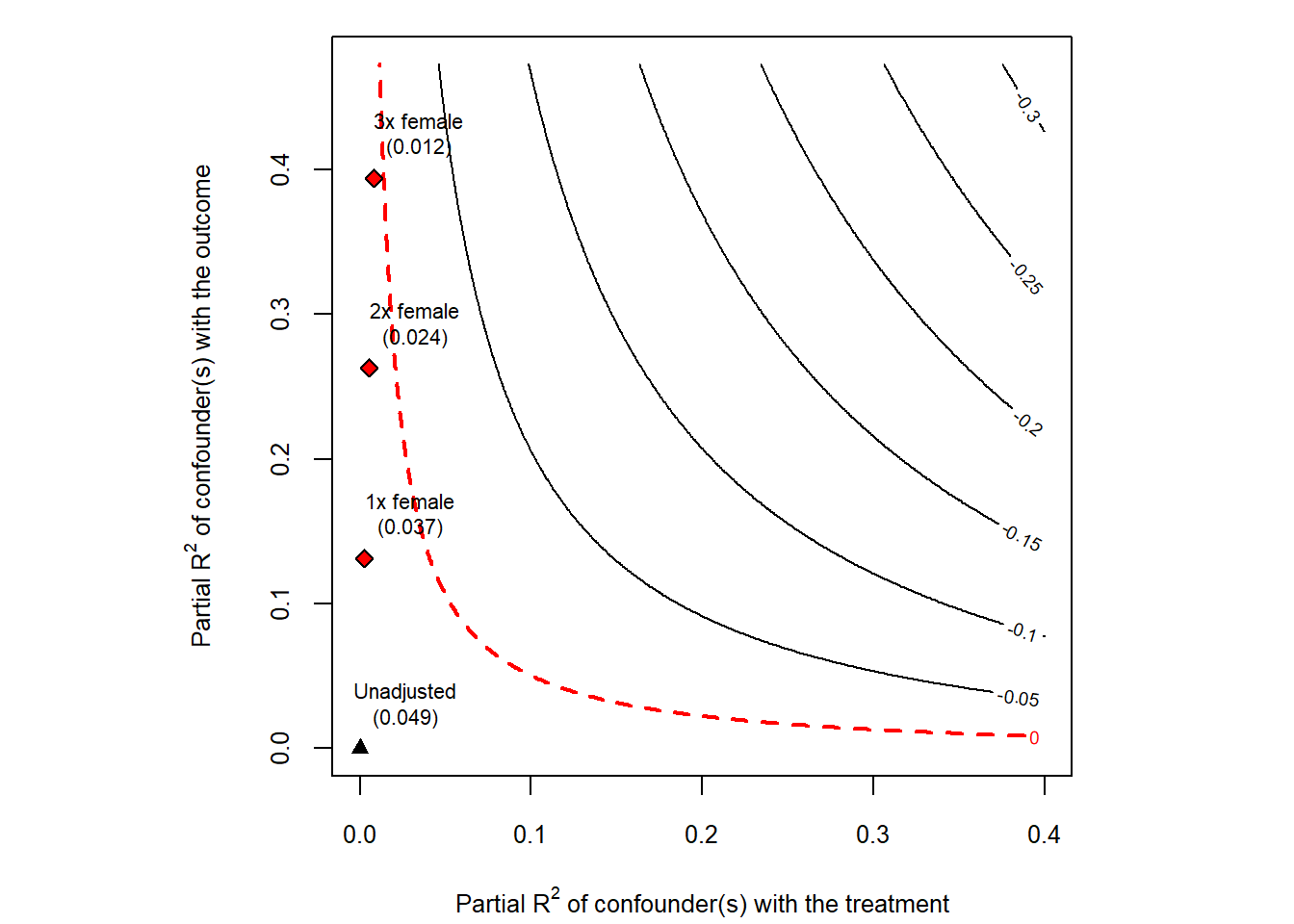
#| fig-cap: "Contornos de sensibilidad"
#| code-fold: true
plot(sens)
```
### Robustness Value (RV)
```{r}
#| label: rv-interpretation
#| code-fold: false
# El Robustness Value indica qué tan fuerte tendría que ser
# un confusor para reducir el efecto a cero
cat("Robustness Value (q=1):",
round(sens$bounds$r2yz.dx[1], 3), "\n")
cat("\nInterpretación: Un confusor tendría que explicar al menos",
round(sens$bounds$r2yz.dx[1] * 100, 1), "% de la varianza\n",
"residual tanto de X como de Y para eliminar el efecto.\n")
```
## Fórmula de sesgo de confusión
La fórmula de sesgo permite calcular cuánto cambiaría la estimación dado un confusor específico:
$$\text{Sesgo} = \frac{(\text{RR}_{UY} - 1) \times (\text{RR}_{UX} - 1)}{\text{RR}_{UY} + (\text{RR}_{UX} - 1) \times P(U)}$$
```{r}
#| label: bias-formula
#| code-fold: false
# Función para calcular sesgo
calcular_sesgo <- function(rr_uy, rr_ux, p_u = 0.5) {
# Fórmula simplificada
bias <- (rr_uy - 1) * (rr_ux - 1) /
(rr_uy + (rr_ux - 1) * p_u)
return(bias)
}
# Ejemplo: ¿Cuánto sesgo introduciría un confusor con RR=1.5
# con exposición y resultado?
sesgo <- calcular_sesgo(rr_uy = 1.5, rr_ux = 1.5)
cat("Sesgo aproximado:", round(sesgo, 3), "\n")
```
## Análisis de sensibilidad para IPTW
```{r}
#| label: sens-iptw
#| code-fold: false
# Simulación con confusor no medido
set.seed(606)
n <- 2000
# Confusor medido
C_medido <- rnorm(n)
# Confusor NO medido
U <- rnorm(n)
# Exposición
prob_X <- plogis(-1 + 0.5 * C_medido + 0.8 * U)
X <- rbinom(n, 1, prob_X)
# Resultado
Y <- 2 + 3 * X + 1.5 * C_medido + 2 * U + rnorm(n)
datos_sens <- data.frame(C_medido, U, X, Y)
# Efecto verdadero (controlando U)
efecto_verdadero <- coef(lm(Y ~ X + C_medido + U, data = datos_sens))["X"]
# Efecto sin U (sesgado)
efecto_sesgado <- coef(lm(Y ~ X + C_medido, data = datos_sens))["X"]
# IPTW sin U
library(WeightIt)
pesos <- weightit(X ~ C_medido, data = datos_sens, method = "ps")
efecto_iptw <- coef(lm(Y ~ X, data = datos_sens, weights = pesos$weights))["X"]
cat("Efecto verdadero (con U):", round(efecto_verdadero, 3), "\n")
cat("Efecto sin U (OLS):", round(efecto_sesgado, 3), "\n")
cat("Efecto IPTW (sin U):", round(efecto_iptw, 3), "\n")
cat("Sesgo por U:", round(efecto_iptw - efecto_verdadero, 3), "\n")
```
## Comunicando resultados de sensibilidad
### Buenas prácticas
1. **Reportar E-values** para el efecto y su intervalo de confianza
2. **Comparar con confusores conocidos**: ¿Es plausible un confusor tan fuerte?
3. **Usar benchmarks**: Comparar con la fuerza de confusores medidos
4. **Ser transparente** sobre las limitaciones
### Ejemplo de reporte
```{r}
#| label: reporting-example
#| code-fold: false
# Supongamos un RR observado
rr_obs <- 1.8
rr_lo <- 1.3
rr_hi <- 2.4
# E-values
ev <- evalues.RR(est = rr_obs, lo = rr_lo, hi = rr_hi)
cat("REPORTE DE SENSIBILIDAD\n")
cat("=======================\n\n")
cat("RR observado: ", rr_obs, " (IC 95%: ", rr_lo, "-", rr_hi, ")\n\n", sep = "")
cat("E-value para el estimado puntual:", round(ev["E-values", "point"], 2), "\n")
cat("E-value para el límite inferior del IC:", round(ev["E-values", "lower"], 2), "\n\n")
cat("Interpretación: Para explicar completamente la asociación observada,\n")
cat("un confusor no medido tendría que estar asociado con tanto la\n")
cat("exposición como el resultado con un RR de al menos",
round(ev["E-values", "point"], 2), ".\n\n")
cat("Para mover el IC inferior a 1.0, la asociación del confusor\n")
cat("tendría que ser de al menos RR =", round(ev["E-values", "lower"], 2), ".\n")
```
## Ejercicios
::: {.callout-tip}
## Ejercicio 1
Un estudio observacional encuentra que el consumo de vegetales está asociado con menor mortalidad (HR = 0.75, IC 95%: 0.65-0.85).
1. Calcula el E-value
2. ¿Qué tan fuerte tendría que ser un confusor para explicar esto?
3. Considera confusores plausibles (nivel socioeconómico, acceso a salud)
:::
::: {.callout-tip}
## Ejercicio 2
Usando `sensemakr`, realiza un análisis de sensibilidad completo para un modelo de tu elección. Interpreta los resultados y determina si el efecto es robusto.
:::
## Resumen
- El análisis de sensibilidad evalúa la robustez de hallazgos causales
- El E-value cuantifica la fuerza mínima de un confusor para explicar el efecto
- `sensemakr` proporciona visualizaciones y métricas avanzadas
- Siempre comparar con la fuerza de confusores conocidos
- Reportar transparentemente las limitaciones del estudio
## Referencias {.unnumbered}