# Sesgo de Selección {#sec-selection-bias}
## Objetivos de aprendizaje
Al finalizar este capítulo, serás capaz de:
- Definir sesgo de selección desde una perspectiva causal
- Identificar el sesgo de colisionador
- Reconocer diferentes tipos de sesgo de selección
- Proponer estrategias para mitigar estos sesgos
## ¿Qué es el sesgo de selección?
El **sesgo de selección** ocurre cuando la asociación entre exposición y resultado difiere entre los participantes del estudio y la población objetivo.
::: {.callout-important}
## Perspectiva causal
Desde el marco de DAGs, el sesgo de selección surge cuando condicionamos en un **collider** o en descendientes de un collider.
:::
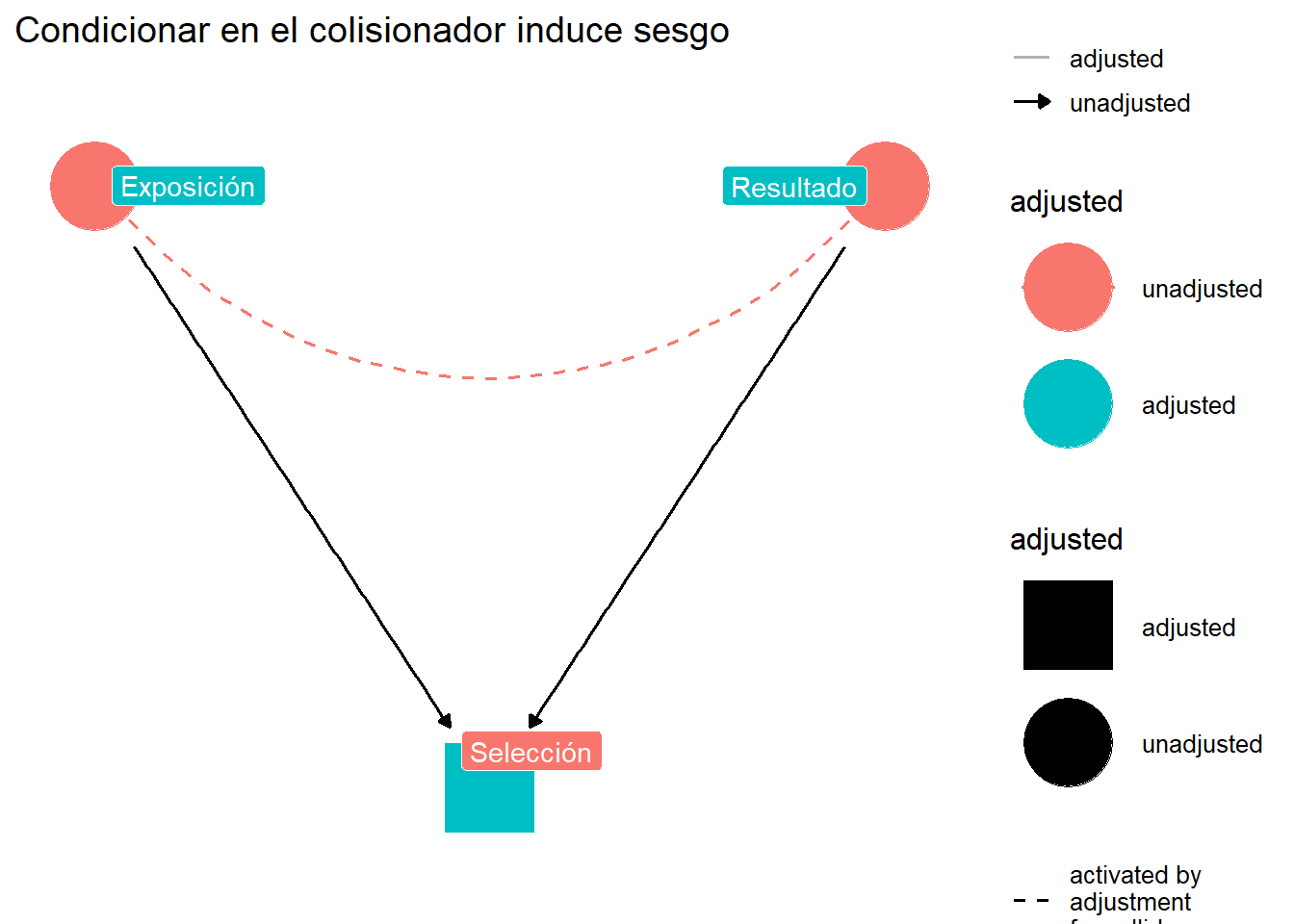
## El sesgo de colisionador
Un **colisionador** es una variable que es efecto común de dos o más variables.
```{r}
#| label: fig-collider-bias
#| fig-cap: "Sesgo de colisionador: condicionar en S abre el camino X → S ← Y"
#| code-fold: true
library(ggdag)
library(ggplot2)
collider_dag <- dagify(
S ~ X + Y,
coords = list(
x = c(X = 0, Y = 2, S = 1),
y = c(X = 0, Y = 0, S = -0.5)
),
labels = c(
X = "Exposición",
Y = "Resultado",
S = "Selección"
)
)
ggdag_adjust(collider_dag, var = "S",
text = FALSE, use_labels = "label") +
theme_dag() +
labs(title = "Condicionar en el colisionador induce sesgo")
```
### Ejemplo: La paradoja del índice de colisión
```{r}
#| label: collider-example
#| code-fold: false
set.seed(789)
n <- 10000
# Habilidad académica y habilidad deportiva (independientes)
academico <- rnorm(n, 0, 1)
deportivo <- rnorm(n, 0, 1)
# Admisión basada en ambas (collider)
admitido <- (academico + deportivo) > 1
# En la población general
cor(academico, deportivo)
# Entre los admitidos solamente
cor(academico[admitido], deportivo[admitido])
```
::: {.callout-note}
## Interpretación
Aunque las habilidades son independientes en la población, entre los admitidos aparece una correlación **negativa**. Esto es porque si una persona con alta habilidad académica fue admitida, no necesita alta habilidad deportiva (y viceversa).
:::
## Tipos de sesgo de selección
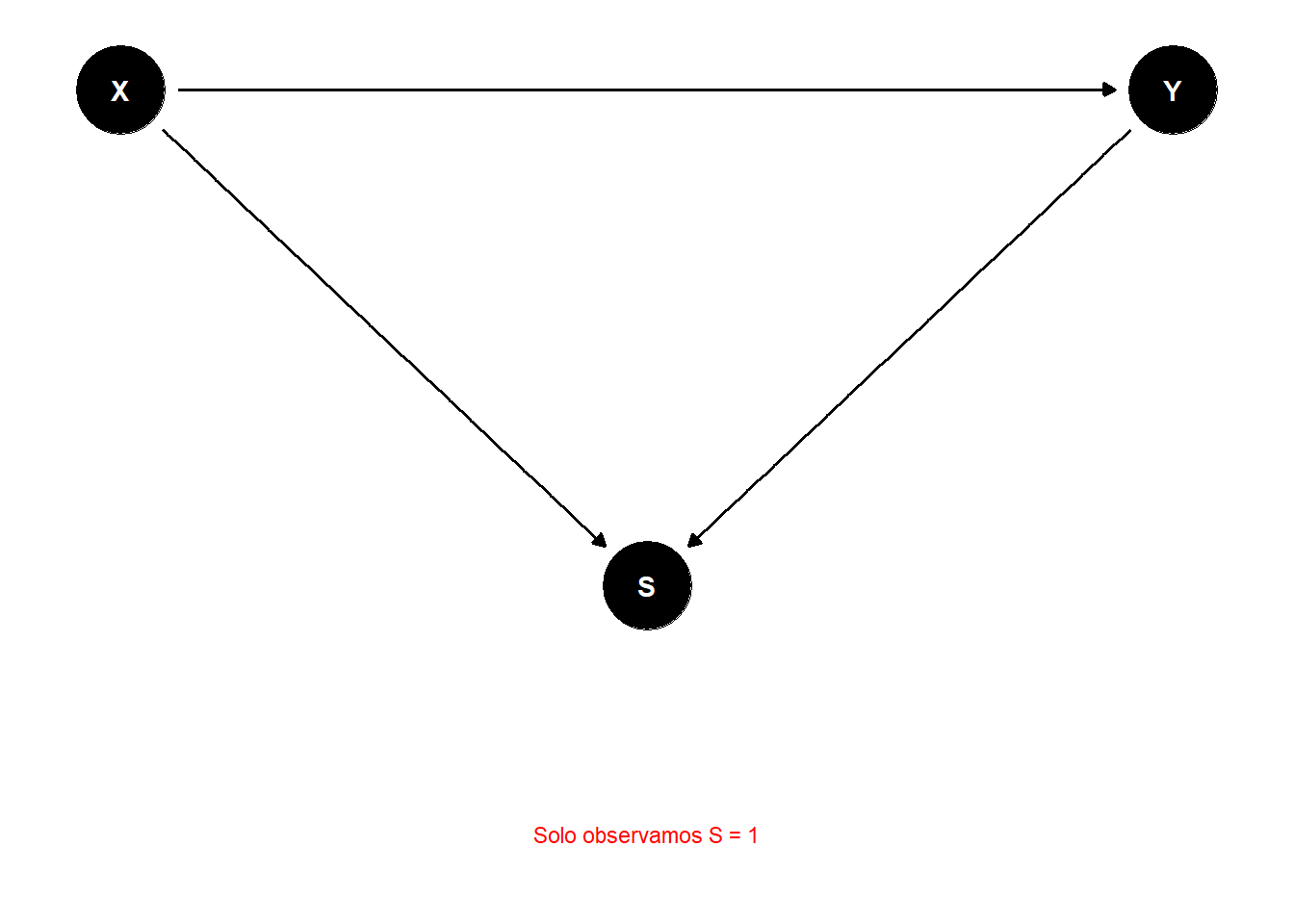
### 1. Sesgo de participación
Ocurre cuando la participación en el estudio depende de la exposición y el resultado.
```{r}
#| label: fig-participation-bias
#| fig-cap: "Sesgo de participación"
#| code-fold: true
part_dag <- dagify(
Y ~ X,
S ~ X + Y,
coords = list(
x = c(X = 0, Y = 2, S = 1),
y = c(X = 0, Y = 0, S = -1)
)
)
ggdag(part_dag) +
theme_dag() +
annotate("text", x = 1, y = -1.5,
label = "Solo observamos S = 1",
size = 3, color = "red")
```
### 2. Sesgo de pérdida de seguimiento
En estudios longitudinales, la pérdida de seguimiento puede estar relacionada con exposición y resultado.
```{r}
#| label: loss-to-followup
#| code-fold: false
# Simulación de pérdida de seguimiento
set.seed(101)
n <- 2000
datos_fup <- data.frame(
tratamiento = rbinom(n, 1, 0.5)
)
# El resultado verdadero
datos_fup$resultado_verdadero <- 50 - 10 * datos_fup$tratamiento +
rnorm(n, 0, 15)
# Pérdida de seguimiento más probable en no tratados con mal resultado
prob_perdida <- plogis(-2 + 1.5 * (1 - datos_fup$tratamiento) -
0.05 * datos_fup$resultado_verdadero)
datos_fup$perdido <- rbinom(n, 1, prob_perdida)
# Resultado observado
datos_fup$resultado_observado <- ifelse(datos_fup$perdido == 1,
NA,
datos_fup$resultado_verdadero)
# Efecto verdadero
efecto_verdadero <- mean(datos_fup$resultado_verdadero[datos_fup$tratamiento == 1]) -
mean(datos_fup$resultado_verdadero[datos_fup$tratamiento == 0])
# Efecto observado (sesgado)
observados <- datos_fup[!is.na(datos_fup$resultado_observado), ]
efecto_observado <- mean(observados$resultado_observado[observados$tratamiento == 1]) -
mean(observados$resultado_observado[observados$tratamiento == 0])
cat("Efecto verdadero:", round(efecto_verdadero, 2), "\n")
cat("Efecto observado:", round(efecto_observado, 2), "\n")
cat("Sesgo:", round(efecto_observado - efecto_verdadero, 2), "\n")
```
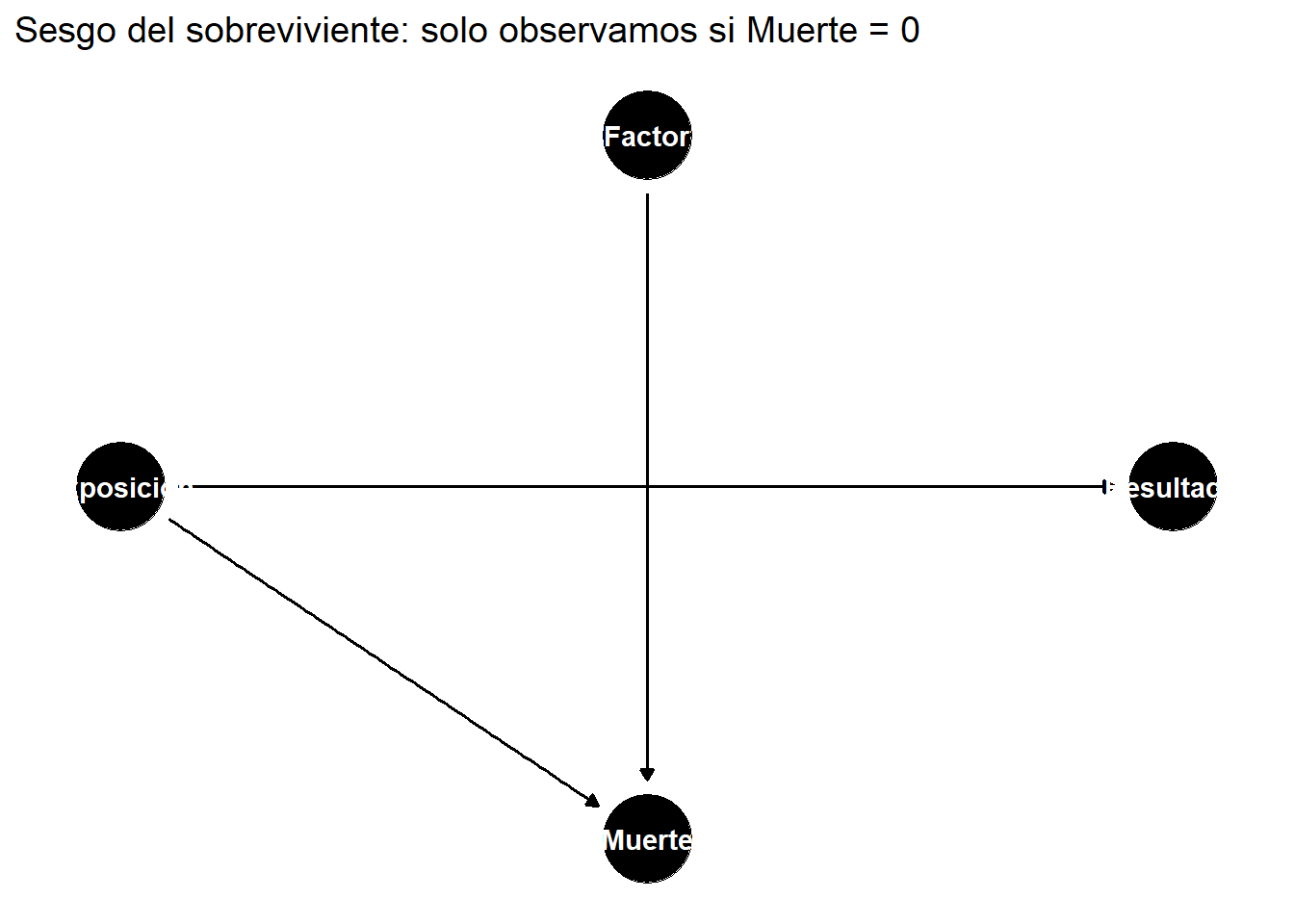
### 3. Sesgo del sobreviviente
Estudiamos solo a quienes "sobrevivieron" a un proceso de selección.
```{r}
#| label: fig-survivor-bias
#| fig-cap: "Sesgo del sobreviviente"
#| code-fold: true
surv_dag <- dagify(
Muerte ~ Exposicion + Factor,
Resultado ~ Exposicion,
coords = list(
x = c(Exposicion = 0, Muerte = 1, Resultado = 2, Factor = 1),
y = c(Exposicion = 0, Muerte = -0.5, Resultado = 0, Factor = 0.5)
)
)
ggdag(surv_dag) +
theme_dag() +
labs(title = "Sesgo del sobreviviente: solo observamos si Muerte = 0")
```
### 4. Sesgo de Berkson
Selección basada en hospitalización u otra condición común.
```{r}
#| label: berkson-bias
#| code-fold: false
# Ejemplo: Enfermedades A y B causan hospitalización
set.seed(202)
n_poblacion <- 50000
poblacion <- data.frame(
enfermedad_A = rbinom(n_poblacion, 1, 0.1), # 10% prevalencia
enfermedad_B = rbinom(n_poblacion, 1, 0.05) # 5% prevalencia
)
# Hospitalización si tiene alguna enfermedad
poblacion$hospitalizado <- as.numeric(
poblacion$enfermedad_A == 1 | poblacion$enfermedad_B == 1
)
# En la población
cat("Correlación en población:",
round(cor(poblacion$enfermedad_A, poblacion$enfermedad_B), 4), "\n")
# Entre hospitalizados
hospitalizados <- poblacion[poblacion$hospitalizado == 1, ]
cat("Correlación entre hospitalizados:",
round(cor(hospitalizados$enfermedad_A, hospitalizados$enfermedad_B), 4), "\n")
```
## Estrategias de mitigación
### 1. Ponderación por probabilidad de selección
Si conocemos los factores de selección, podemos usar **ponderación por inverso de la probabilidad de selección** (IPWS).
```{r}
#| label: ipws
#| code-fold: false
# Usando los datos de pérdida de seguimiento
datos_fup$prob_no_perdida <- 1 - prob_perdida
datos_fup$peso <- 1 / datos_fup$prob_no_perdida
# Análisis ponderado (solo en observados)
observados$peso <- datos_fup$peso[!is.na(datos_fup$resultado_observado)]
efecto_ponderado <- weighted.mean(
observados$resultado_observado[observados$tratamiento == 1],
observados$peso[observados$tratamiento == 1]) -
weighted.mean(
observados$resultado_observado[observados$tratamiento == 0],
observados$peso[observados$tratamiento == 0])
cat("Efecto verdadero:", round(efecto_verdadero, 2), "\n")
cat("Efecto ponderado:", round(efecto_ponderado, 2), "\n")
```
### 2. Análisis de sensibilidad
Evaluar cómo diferentes asunciones sobre la selección afectan los resultados.
### 3. Diseño del estudio
- Minimizar pérdida de seguimiento
- Recopilar información sobre los que no participan
- Usar muestreo representativo
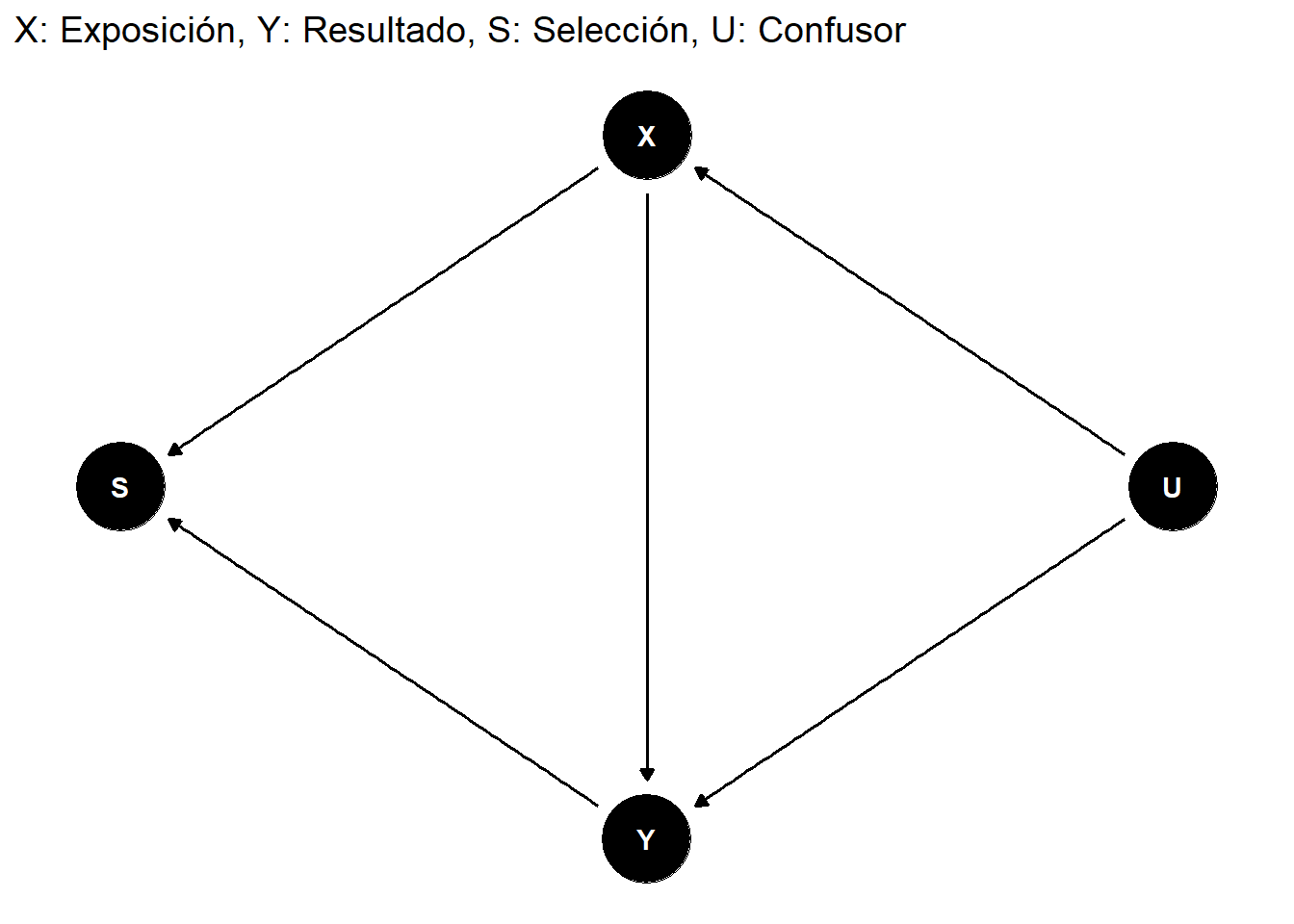
## Identificación usando DAGs
```{r}
#| label: fig-selection-dag-full
#| fig-cap: "DAG completo con mecanismo de selección"
#| code-fold: true
library(dagitty)
full_dag <- dagitty("dag {
X -> Y
U -> X
U -> Y
X -> S
Y -> S
}")
ggdag(full_dag) +
theme_dag() +
labs(title = "X: Exposición, Y: Resultado, S: Selección, U: Confusor")
```
```{r}
#| label: selection-adjustment
#| code-fold: false
# Verificar si el efecto es identificable
# dado que condicionamos en S
full_dag <- dagitty("dag {
X -> Y
U -> X
U -> Y
X -> S
Y -> S
}")
# ¿Qué debemos ajustar si estamos condicionando en S?
cat("Conjuntos de ajuste cuando S está condicionado:\n")
print(adjustmentSets(full_dag, exposure = "X", outcome = "Y",
type = "all"))
```
## Ejercicios
::: {.callout-tip}
## Ejercicio 1
Un estudio hospitalario encuentra que los pacientes con diabetes tienen menor riesgo de enfermedad pulmonar. Dibuja un DAG y explica por qué esto podría ser sesgo de Berkson.
:::
::: {.callout-tip}
## Ejercicio 2
En un ensayo clínico, 30% de los pacientes en el grupo placebo abandonan vs. 10% en el grupo tratamiento. Simula este escenario y cuantifica el sesgo resultante.
:::
## Resumen
- El sesgo de selección distorsiona la asociación entre exposición y resultado
- Desde la perspectiva de DAGs, surge al condicionar en un collider
- Incluye: sesgo de participación, pérdida de seguimiento, sobreviviente y Berkson
- La ponderación por probabilidad de selección puede corregir el sesgo
- El diseño cuidadoso del estudio es la mejor prevención
## Referencias {.unnumbered}