# Control de Confusión {#sec-confounding}
## Objetivos de aprendizaje
Al finalizar este capítulo, serás capaz de:
- Definir confusión y sus consecuencias
- Aplicar métodos de estratificación
- Implementar matching (emparejamiento)
- Utilizar ponderación por propensity score
## ¿Qué es la confusión?
La **confusión** ocurre cuando una variable externa está asociada tanto con la exposición como con el resultado, distorsionando la estimación del efecto causal.
::: {.callout-warning}
## Consecuencia
Sin control adecuado de la confusión, podemos:
- Encontrar una asociación donde no existe efecto causal
- No detectar un efecto causal real
- Subestimar o sobreestimar la magnitud del efecto
:::
## Métodos para controlar confusión
### 1. Estratificación
La **estratificación** divide los datos en grupos homogéneos según el confusor.
```{r}
#| label: stratification-example
#| code-fold: false
# Simular datos
set.seed(123)
n <- 1000
# Confusor: edad (0 = joven, 1 = mayor)
edad <- rbinom(n, 1, 0.5)
# Exposición influenciada por edad
tratamiento <- rbinom(n, 1, 0.3 + 0.4 * edad)
# Resultado influenciado por ambos
resultado <- 50 + 10 * edad + 5 * tratamiento + rnorm(n, 0, 5)
datos <- data.frame(edad, tratamiento, resultado)
# Efecto crudo
cat("Efecto crudo:",
round(mean(resultado[tratamiento == 1]) -
mean(resultado[tratamiento == 0]), 2), "\n")
# Efecto estratificado
efecto_jovenes <- mean(resultado[tratamiento == 1 & edad == 0]) -
mean(resultado[tratamiento == 0 & edad == 0])
efecto_mayores <- mean(resultado[tratamiento == 1 & edad == 1]) -
mean(resultado[tratamiento == 0 & edad == 1])
cat("Efecto en jóvenes:", round(efecto_jovenes, 2), "\n")
cat("Efecto en mayores:", round(efecto_mayores, 2), "\n")
```
### 2. Matching (Emparejamiento)
El **matching** empareja individuos tratados y no tratados con características similares.
```{r}
#| label: matching-example
#| code-fold: false
library(MatchIt)
# Datos más complejos
set.seed(456)
n <- 500
datos_match <- data.frame(
edad = rnorm(n, 50, 10),
imc = rnorm(n, 25, 5),
sexo = rbinom(n, 1, 0.5)
)
# Probabilidad de tratamiento
prob_trat <- plogis(-2 + 0.05 * datos_match$edad +
0.1 * datos_match$imc)
datos_match$tratamiento <- rbinom(n, 1, prob_trat)
# Resultado
datos_match$resultado <- 100 +
0.5 * datos_match$edad +
2 * datos_match$imc -
5 * datos_match$tratamiento +
rnorm(n, 0, 10)
# Matching
match_out <- matchit(tratamiento ~ edad + imc + sexo,
data = datos_match,
method = "nearest",
ratio = 1)
summary(match_out)
```
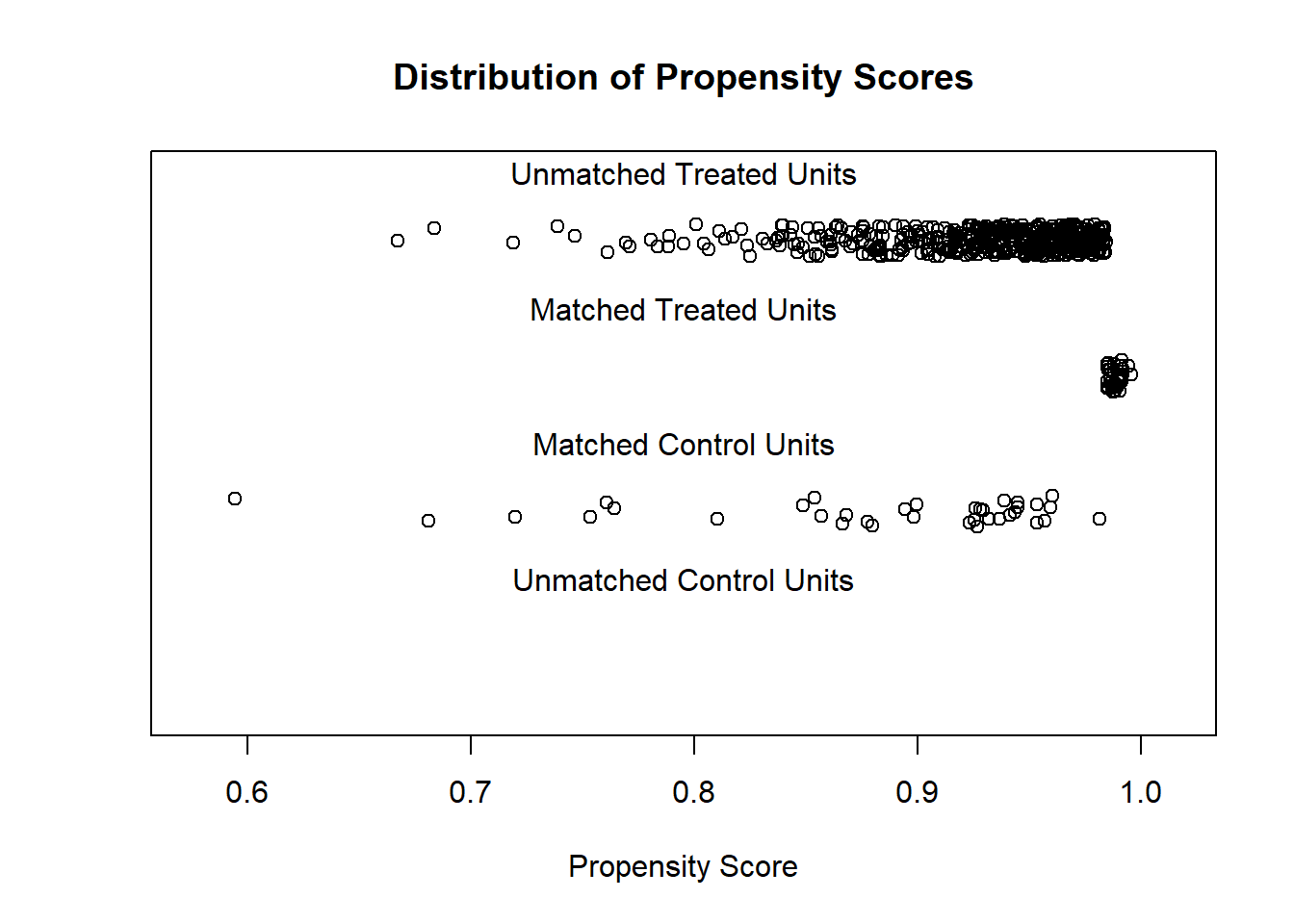
#### Balance después del matching
```{r}
#| label: fig-balance
#| fig-cap: "Balance de covariables antes y después del matching"
#| code-fold: true
library(ggplot2)
plot(match_out, type = "jitter", interactive = FALSE)
```
#### Estimación del efecto
```{r}
#| label: matching-effect
#| code-fold: false
# Obtener datos emparejados
datos_emparejados <- match.data(match_out)
# Efecto en datos emparejados
modelo_match <- lm(resultado ~ tratamiento,
data = datos_emparejados,
weights = weights)
summary(modelo_match)$coefficients["tratamiento", ]
```
### 3. Propensity Score
El **propensity score** es la probabilidad de recibir el tratamiento dado las covariables.
$$e(X) = P(T = 1 | X)$$
```{r}
#| label: propensity-score
#| code-fold: false
# Estimar propensity score
ps_model <- glm(tratamiento ~ edad + imc + sexo,
data = datos_match,
family = binomial)
datos_match$ps <- predict(ps_model, type = "response")
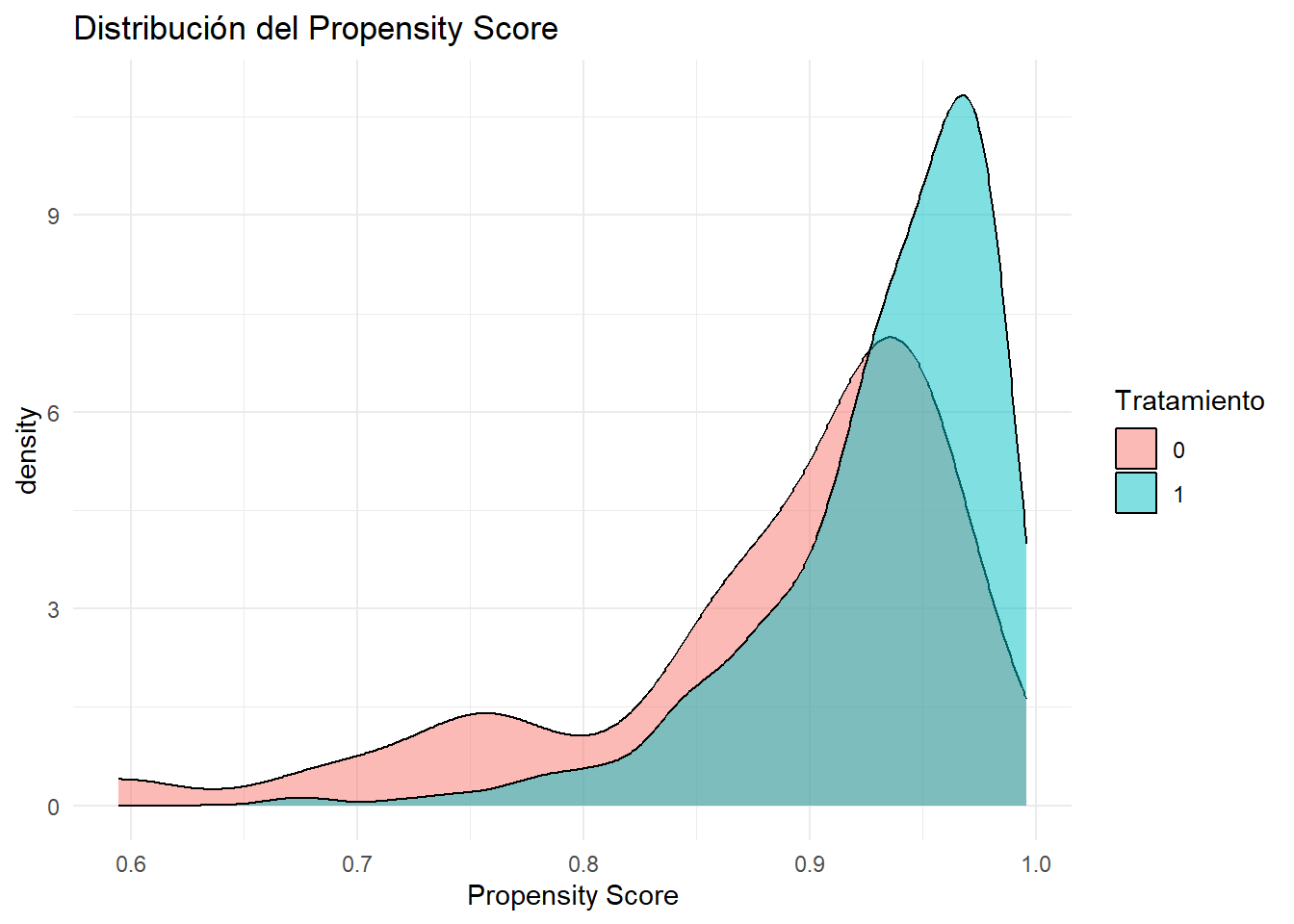
# Visualizar distribución
ggplot(datos_match, aes(x = ps, fill = factor(tratamiento))) +
geom_density(alpha = 0.5) +
labs(title = "Distribución del Propensity Score",
x = "Propensity Score",
fill = "Tratamiento") +
theme_minimal()
```
### 4. Ponderación (IPTW)
La **ponderación por el inverso del propensity score** (IPTW) crea una pseudo-población donde tratamiento y covariables son independientes.
$$w_i = \frac{T_i}{e(X_i)} + \frac{1 - T_i}{1 - e(X_i)}$$
```{r}
#| label: iptw
#| code-fold: false
library(WeightIt)
# Calcular pesos
pesos <- weightit(tratamiento ~ edad + imc + sexo,
data = datos_match,
method = "ps",
estimand = "ATE")
summary(pesos)
# Modelo ponderado
modelo_iptw <- lm(resultado ~ tratamiento,
data = datos_match,
weights = pesos$weights)
summary(modelo_iptw)$coefficients["tratamiento", ]
```
## Comparación de métodos
| Método | Ventajas | Desventajas |
|--------|----------|-------------|
| Estratificación | Simple, transparente | Solo para pocos confusores |
| Matching | Intuitivo, balance visible | Pérdida de muestra |
| PS Matching | Reduce dimensionalidad | Depende del modelo de PS |
| IPTW | Usa toda la muestra | Pesos extremos posibles |
## Diagnósticos importantes
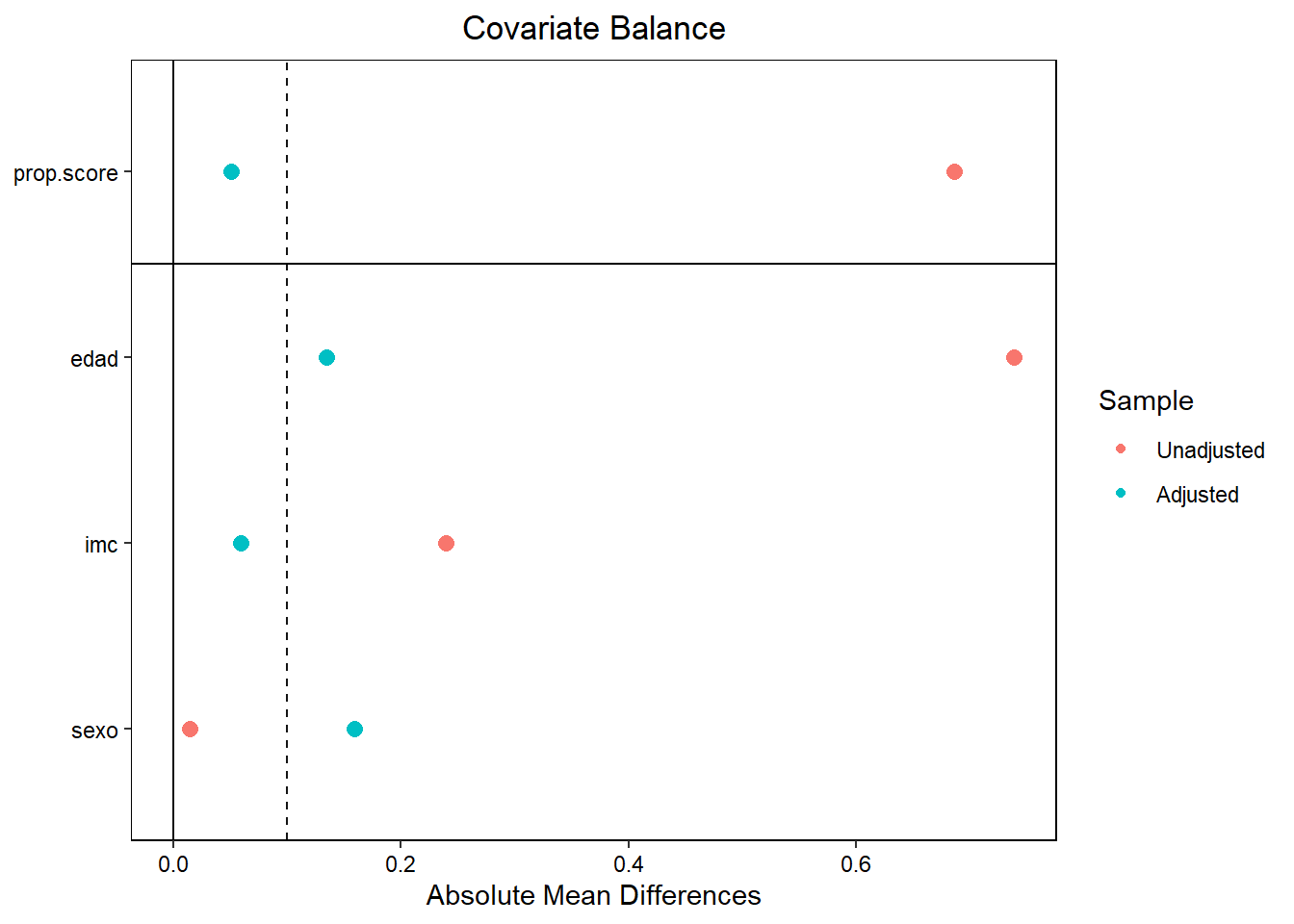
### Balance de covariables
```{r}
#| label: fig-love-plot
#| fig-cap: "Love plot: comparación de balance"
#| code-fold: true
library(cobalt)
love.plot(pesos,
thresholds = c(m = 0.1),
abs = TRUE,
var.order = "unadjusted")
```
### Distribución de pesos
```{r}
#| label: weight-diagnostics
#| code-fold: false
summary(pesos$weights)
# Pesos extremos pueden indicar violación de positividad
cat("Pesos > 10:", sum(pesos$weights > 10), "\n")
```
## Ejercicios
::: {.callout-tip}
## Ejercicio 1
Usando el dataset simulado, compara los resultados de:
1. Análisis crudo
2. Matching por edad e IMC
3. IPTW
¿Cuál se acerca más al efecto verdadero (-5)?
:::
::: {.callout-tip}
## Ejercicio 2
Evalúa el impacto de diferentes métodos de matching (nearest, optimal, genetic) en el balance y la estimación del efecto.
:::
## Resumen
- La confusión distorsiona las estimaciones de efectos causales
- La estratificación es útil para pocos confusores
- El matching empareja individuos similares
- El propensity score resume múltiples confusores en un solo número
- IPTW permite usar toda la muestra
- Siempre verificar el balance después del ajuste
## Referencias {.unnumbered}