8 Análisis de Mediación

8.1 Objetivos de aprendizaje

Al finalizar este capítulo, serás capaz de:

Distinguir entre efectos directos e indirectos
Definir efectos de mediación causal (NDE, NIE)
Identificar las asunciones para mediación
Aplicar el paquete mediation en R

8.2 ¿Qué es la mediación?

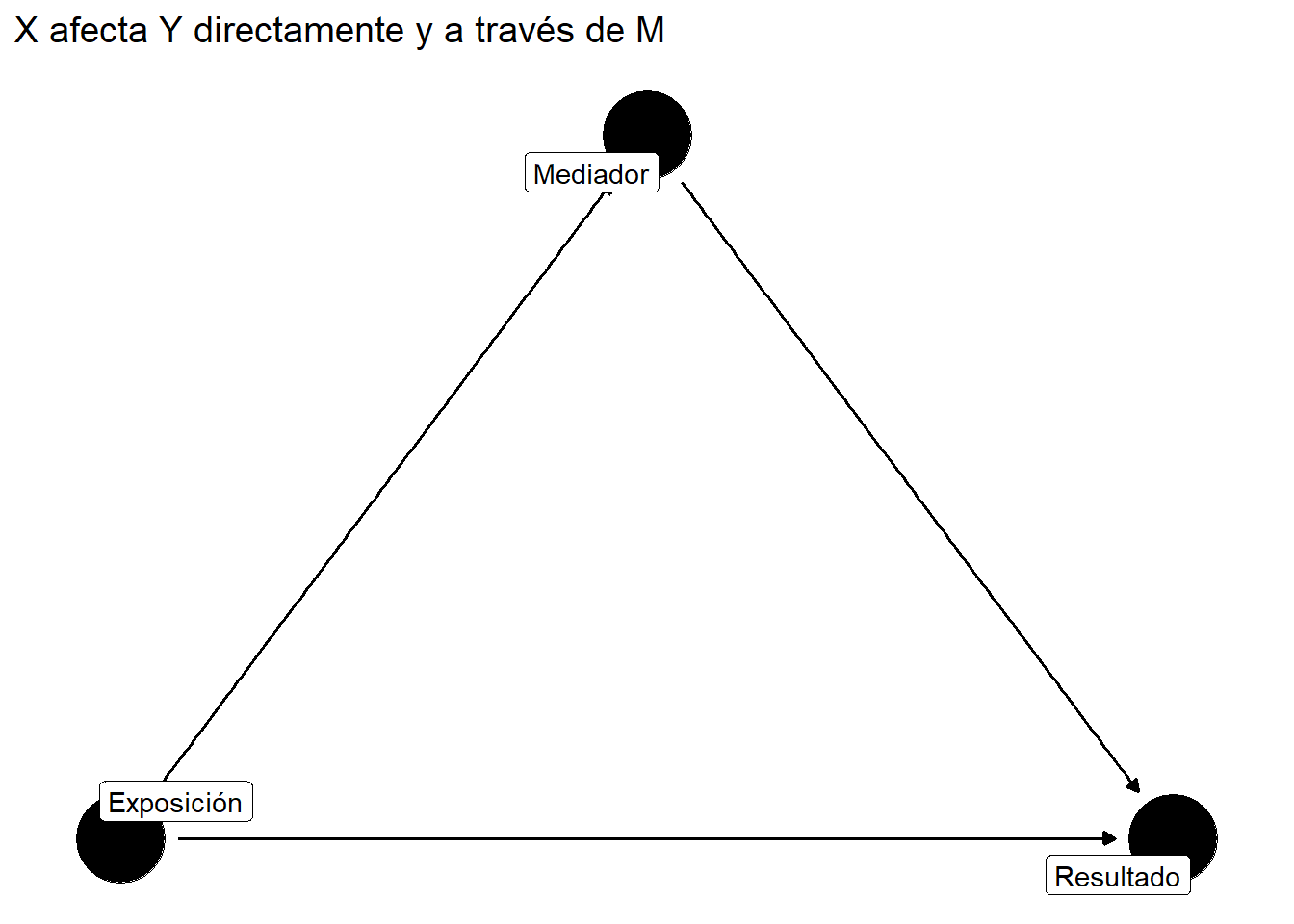
La mediación examina cómo o por qué una exposición afecta un resultado. El efecto puede ser:

Directo: X → Y
Indirecto: X → M → Y (a través de un mediador)

Código

library(ggdag)
library(ggplot2)

med_dag <- dagify(
  M ~ X,
  Y ~ X + M,
  coords = list(
    x = c(X = 0, M = 1, Y = 2),
    y = c(X = 0, M = 0.5, Y = 0)
  ),
  labels = c(
    X = "Exposición",
    M = "Mediador",
    Y = "Resultado"
  )
)

ggdag(med_dag, text = FALSE, use_labels = "label") +
  theme_dag() +
  labs(title = "X afecta Y directamente y a través de M")

Figura 8.1: Diagrama de mediación simple

8.3 Definiciones causales

8.3.1 Efectos naturales (NDE y NIE)

Efecto Directo Natural (NDE): Efecto de X sobre Y manteniendo M en el nivel que habría tenido sin la exposición
Efecto Indirecto Natural (NIE): Efecto de cambiar M desde el nivel sin exposición al nivel con exposición, manteniendo X fijo

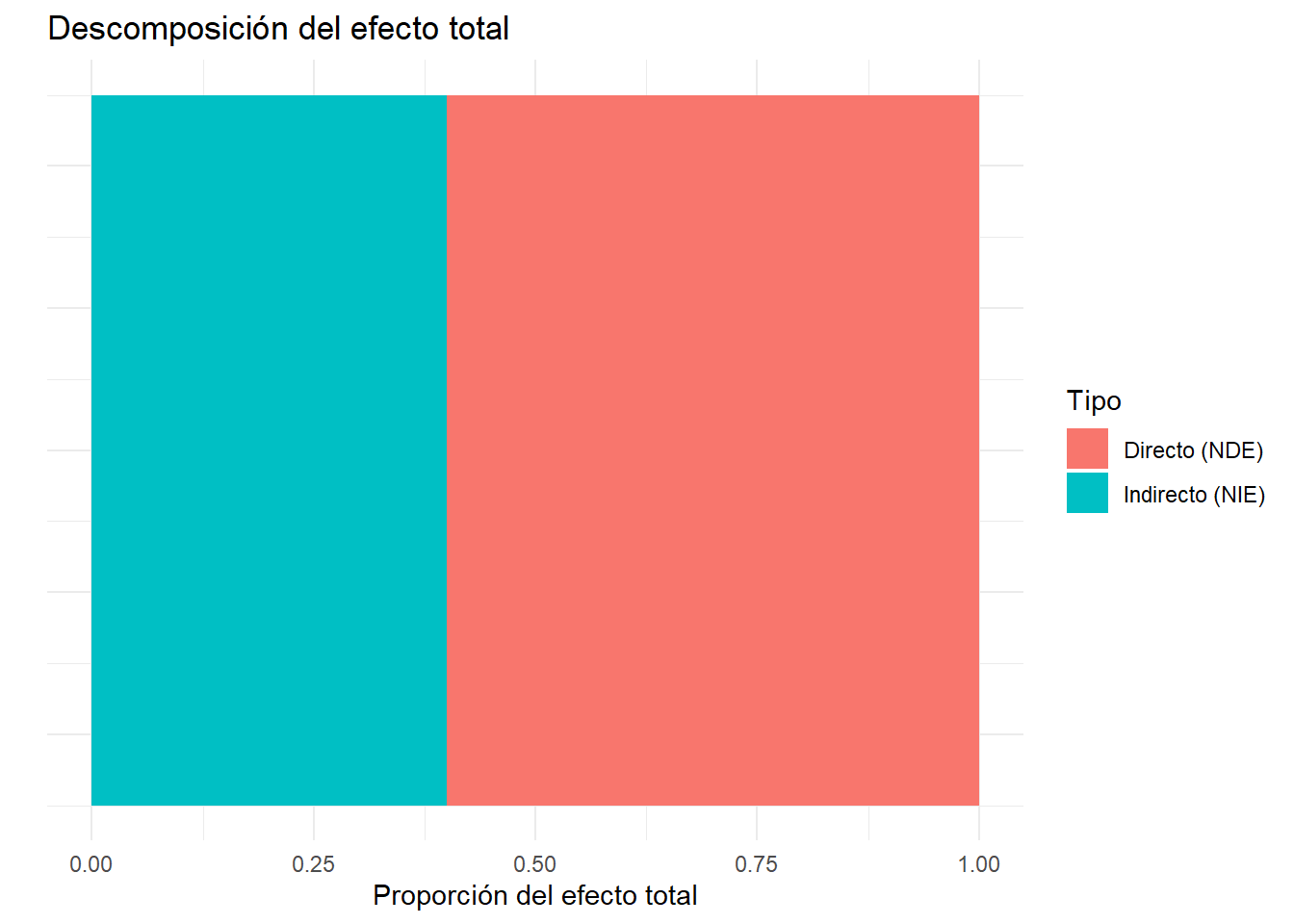
\[\text{Efecto Total} = \text{NDE} + \text{NIE}\]

Código

library(ggplot2)

# Datos para visualización
efectos <- data.frame(
  Tipo = c("Directo (NDE)", "Indirecto (NIE)"),
  Valor = c(0.6, 0.4),
  ymin = 0,
  ymax = c(0.6, 1.0)
)

ggplot(efectos, aes(x = 1, y = Valor, fill = Tipo)) +
  geom_col(position = "stack", width = 0.5) +
  coord_flip() +
  labs(y = "Proporción del efecto total",
       x = "",
       title = "Descomposición del efecto total") +
  theme_minimal() +
  theme(axis.text.y = element_blank(),
        axis.ticks.y = element_blank())

Figura 8.2: Descomposición del efecto total

8.4 Asunciones para identificación

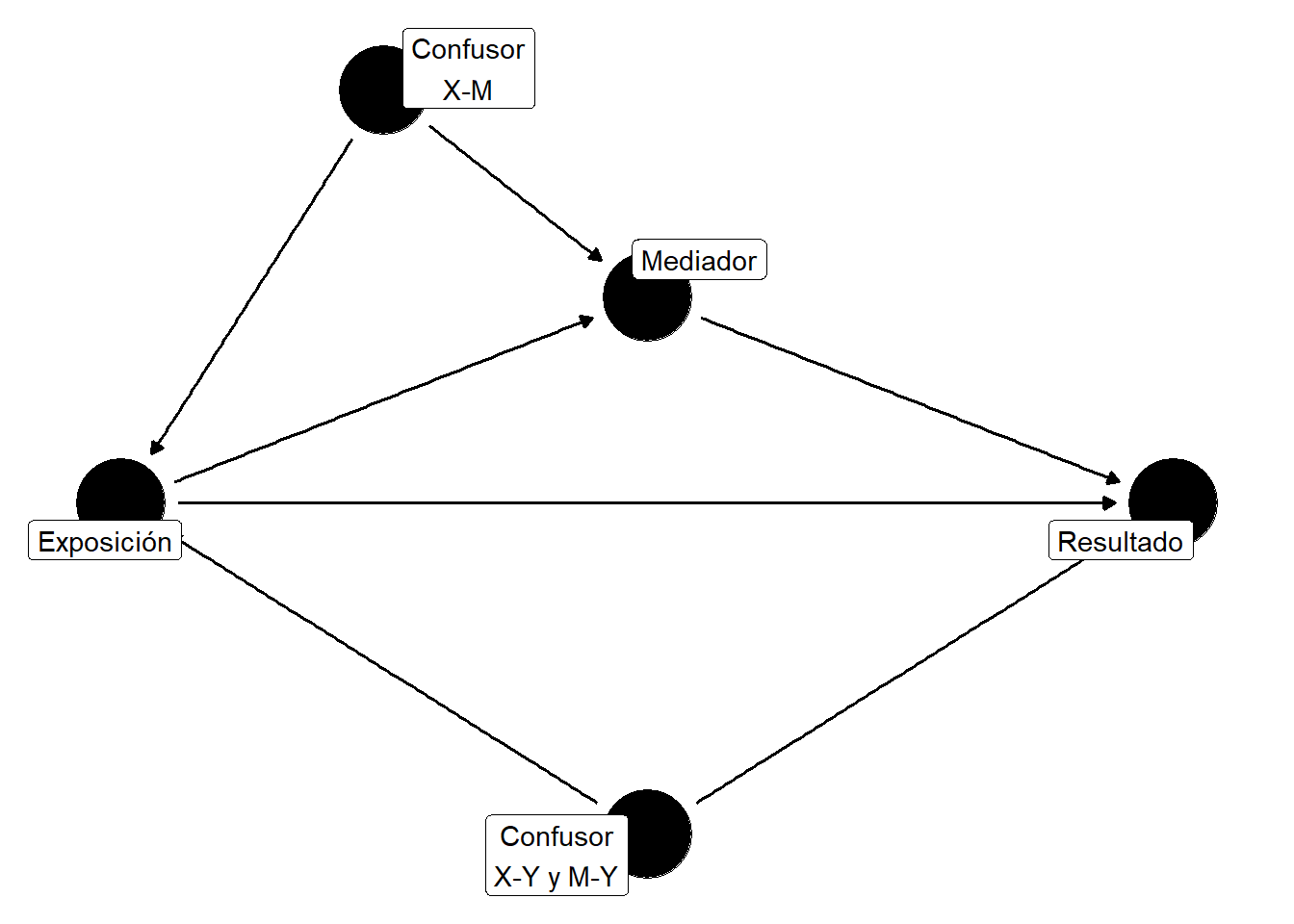
Cuatro asunciones de no confusión

No hay confusión de X → Y
No hay confusión de M → Y
No hay confusión de X → M
No hay confusor de M → Y afectado por X

La cuarta asunción es frecuentemente violada y difícil de verificar.

Código

full_med_dag <- dagify(
  M ~ X + C1,
  Y ~ X + M + C2,
  X ~ C1 + C2,
  coords = list(
    x = c(X = 0, M = 1, Y = 2, C1 = 0.5, C2 = 1),
    y = c(X = 0, M = 0.5, Y = 0, C1 = 1, C2 = -0.8)
  ),
  labels = c(
    X = "Exposición",
    M = "Mediador",
    Y = "Resultado",
    C1 = "Confusor\nX-M",
    C2 = "Confusor\nX-Y y M-Y"
  )
)

ggdag(full_med_dag, text = FALSE, use_labels = "label") +
  theme_dag()

Figura 8.3: Escenario con todas las asunciones satisfechas

8.5 Método de Baron-Kenny (tradicional)

El enfoque clásico usa tres regresiones:

# Simular datos
set.seed(707)
n <- 1000

X <- rnorm(n)  # Exposición
M <- 0.5 * X + rnorm(n, 0, 0.5)  # Mediador
Y <- 0.3 * X + 0.6 * M + rnorm(n, 0, 0.5)  # Resultado

datos_med <- data.frame(X, M, Y)

# Paso 1: Efecto total (X -> Y)
modelo1 <- lm(Y ~ X, data = datos_med)
cat("Efecto total:", round(coef(modelo1)["X"], 3), "\n")

Efecto total: 0.603

# Paso 2: Efecto de X sobre M
modelo2 <- lm(M ~ X, data = datos_med)
cat("Efecto X -> M:", round(coef(modelo2)["X"], 3), "\n")

Efecto X -> M: 0.504

# Paso 3: Efecto de X y M sobre Y
modelo3 <- lm(Y ~ X + M, data = datos_med)
cat("Efecto directo (X -> Y|M):", round(coef(modelo3)["X"], 3), "\n")

Efecto directo (X -> Y|M): 0.306

cat("Efecto M -> Y:", round(coef(modelo3)["M"], 3), "\n")

Efecto M -> Y: 0.59

# Efecto indirecto (producto de coeficientes)
efecto_indirecto <- coef(modelo2)["X"] * coef(modelo3)["M"]
cat("\nEfecto indirecto (a × b):", round(efecto_indirecto, 3), "\n")


Efecto indirecto (a × b): 0.297

8.5.1 Limitaciones del método tradicional

No tiene interpretación causal clara
Asume linearidad
No funciona bien con mediadores o resultados binarios
Intervalos de confianza problemáticos

8.6 Método de mediación causal

El paquete mediation implementa el enfoque de efectos naturales:

library(mediation)

# Modelo para el mediador
modelo_mediador <- lm(M ~ X, data = datos_med)

# Modelo para el resultado
modelo_resultado <- lm(Y ~ X + M, data = datos_med)

# Análisis de mediación
med_out <- mediate(modelo_mediador, modelo_resultado,
                   treat = "X",
                   mediator = "M",
                   boot = TRUE,
                   sims = 500)

summary(med_out)


Causal Mediation Analysis 

Nonparametric Bootstrap Confidence Intervals with the Percentile Method

               Estimate 95% CI Lower 95% CI Upper   p-value    
ACME            0.29717      0.26265      0.33218 < 2.2e-16 ***
ADE             0.30631      0.26522      0.35520 < 2.2e-16 ***
Total Effect    0.60348      0.56832      0.64330 < 2.2e-16 ***
Prop. Mediated  0.49243      0.42951      0.54926 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Sample Size Used: 1000 


Simulations: 500

8.6.1 Interpretación de resultados

cat("=== INTERPRETACIÓN ===\n\n")

=== INTERPRETACIÓN ===

cat("ACME (Average Causal Mediation Effect):", 
    round(med_out$d0, 3), "\n")

ACME (Average Causal Mediation Effect): 0.297

cat("  → Efecto que pasa a través del mediador\n\n")

  → Efecto que pasa a través del mediador

cat("ADE (Average Direct Effect):", 
    round(med_out$z0, 3), "\n")

ADE (Average Direct Effect): 0.306

cat("  → Efecto que NO pasa por el mediador\n\n")

  → Efecto que NO pasa por el mediador

cat("Proporción mediada:", 
    round(med_out$n0, 2), "\n")

Proporción mediada: 0.49

cat("  → ", round(med_out$n0 * 100), "% del efecto total es mediado\n", sep = "")

  → 49% del efecto total es mediado

8.7 Mediación con resultados binarios

# Datos con resultado binario
set.seed(808)
n <- 2000

X <- rbinom(n, 1, 0.5)  # Exposición binaria
M <- plogis(-1 + 1.5 * X) + rnorm(n, 0, 0.2)  # Mediador continuo
M <- pmax(0, pmin(1, M))  # Limitar entre 0 y 1
Y <- rbinom(n, 1, plogis(-1.5 + 0.5 * X + 2 * M))  # Resultado binario

datos_bin <- data.frame(X, M, Y)

# Modelos
mod_med_bin <- lm(M ~ X, data = datos_bin)
mod_out_bin <- glm(Y ~ X + M, data = datos_bin, family = binomial)

# Mediación
med_bin <- mediate(mod_med_bin, mod_out_bin,
                   treat = "X",
                   mediator = "M",
                   boot = TRUE,
                   sims = 200)

summary(med_bin)


Causal Mediation Analysis 

Nonparametric Bootstrap Confidence Intervals with the Percentile Method

                         Estimate 95% CI Lower 95% CI Upper   p-value    
ACME (control)           0.155226     0.116670     0.195889 < 2.2e-16 ***
ACME (treated)           0.165200     0.128907     0.204012 < 2.2e-16 ***
ADE (control)            0.082277     0.029158     0.136139 < 2.2e-16 ***
ADE (treated)            0.092251     0.034054     0.149166 < 2.2e-16 ***
Total Effect             0.247478     0.208113     0.294190 < 2.2e-16 ***
Prop. Mediated (control) 0.627234     0.439330     0.840683 < 2.2e-16 ***
Prop. Mediated (treated) 0.667537     0.493558     0.865155 < 2.2e-16 ***
ACME (average)           0.160213     0.123372     0.200685 < 2.2e-16 ***
ADE (average)            0.087264     0.031540     0.142628 < 2.2e-16 ***
Prop. Mediated (average) 0.647385     0.462488     0.852919 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Sample Size Used: 2000 


Simulations: 200

8.8 Análisis de sensibilidad para mediación

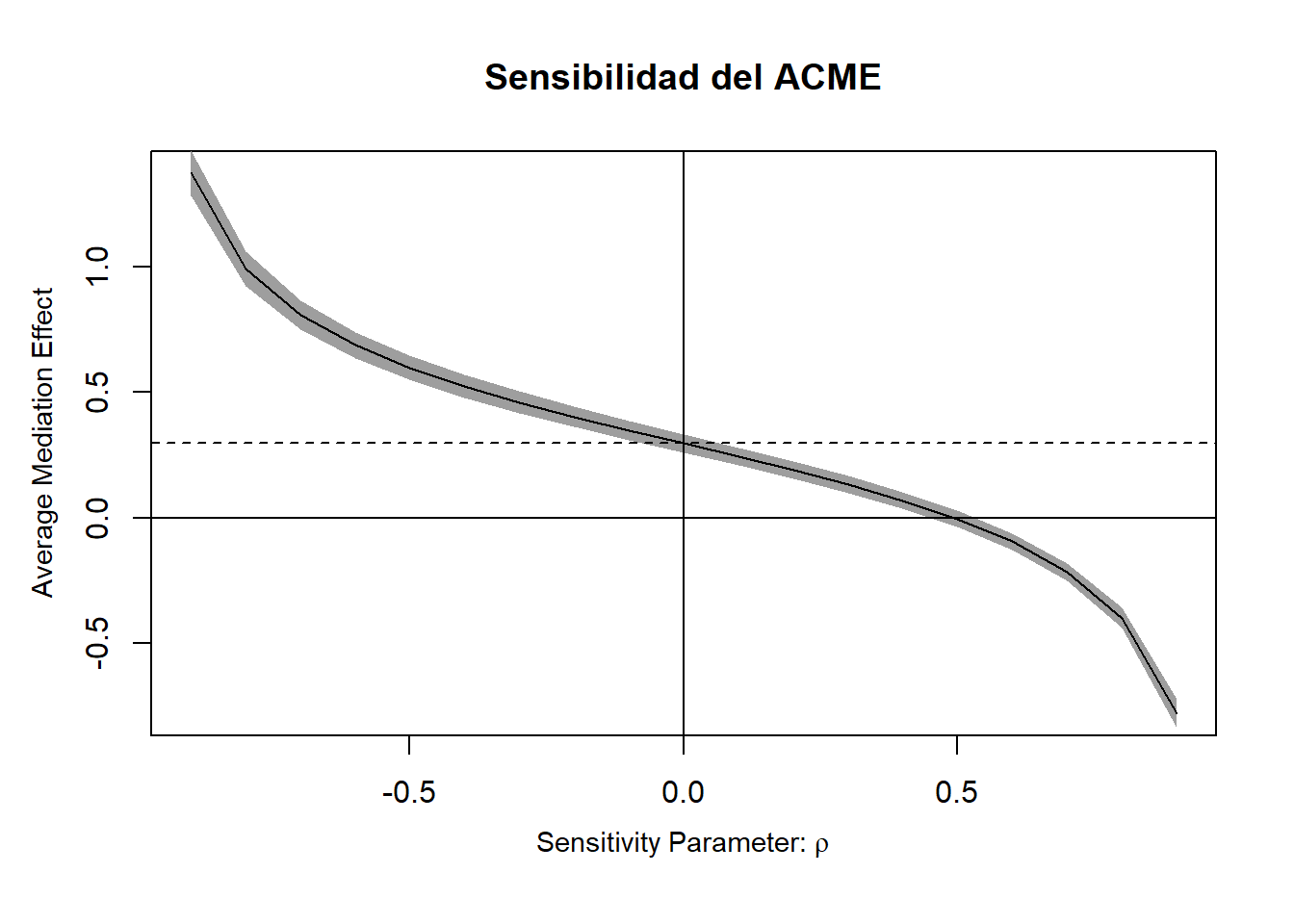
La violación de las asunciones (especialmente la 4ª) puede sesgar las estimaciones. El paquete mediation incluye análisis de sensibilidad:

# Análisis de sensibilidad
sens_med <- medsens(med_out, rho.by = 0.1, sims = 200)
summary(sens_med)


Mediation Sensitivity Analysis for Average Causal Mediation Effect

Sensitivity Region

     Rho    ACME 95% CI Lower 95% CI Upper R^2_M*R^2_Y* R^2_M~R^2_Y~
[1,] 0.5 -0.0041      -0.0365       0.0283         0.25       0.0446

Rho at which ACME = 0: 0.5
R^2_M*R^2_Y* at which ACME = 0: 0.25
R^2_M~R^2_Y~ at which ACME = 0: 0.0446

Código

plot(sens_med, main = "Sensibilidad del ACME")

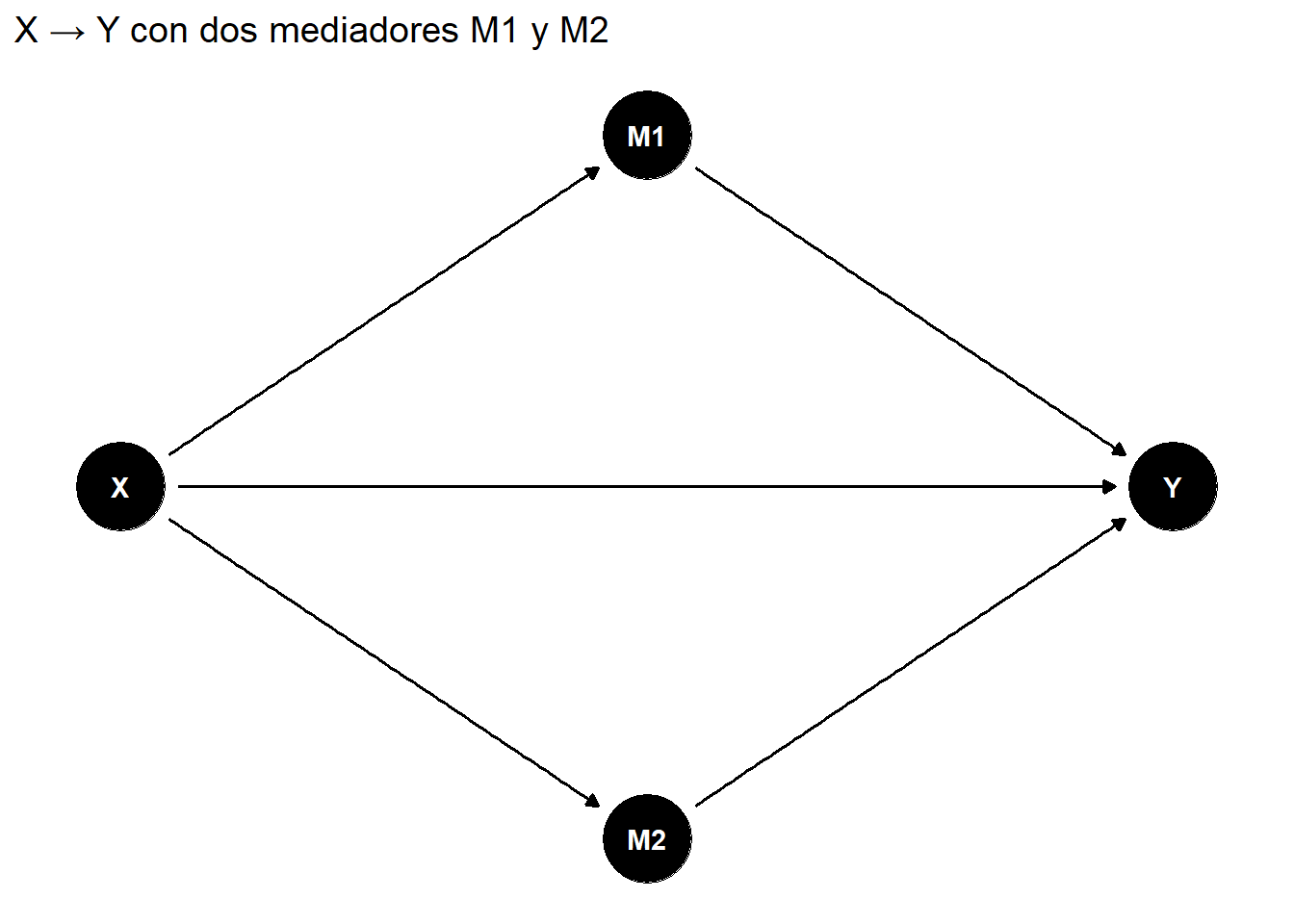
Figura 8.4: Sensibilidad del efecto indirecto

8.9 Múltiples mediadores

Cuando hay varios mediadores, el análisis se complica:

Código

multi_med_dag <- dagify(
  M1 ~ X,
  M2 ~ X,
  Y ~ X + M1 + M2,
  coords = list(
    x = c(X = 0, M1 = 1, M2 = 1, Y = 2),
    y = c(X = 0, M1 = 0.5, M2 = -0.5, Y = 0)
  )
)

ggdag(multi_med_dag) +
  theme_dag() +
  labs(title = "X → Y con dos mediadores M1 y M2")

Complicación

Con múltiples mediadores que pueden afectarse entre sí, los efectos indirectos específicos para cada mediador generalmente no están identificados sin asunciones adicionales.

8.10 Ejercicios

Ejercicio 1

Un programa educativo (X) mejora las calificaciones (Y). Se hipotetiza que el efecto es mediado por horas de estudio (M).

Simula datos bajo este escenario
Estima NDE y NIE
Calcula la proporción mediada
Realiza análisis de sensibilidad

Ejercicio 2

Considera el caso donde el mediador M tiene un confusor U que también está afectado por X (violación de la 4ª asunción). Simula este escenario y muestra cómo sesga las estimaciones.

8.11 Resumen

La mediación descompone el efecto total en directo e indirecto
NDE y NIE tienen interpretación causal clara
Se requieren cuatro asunciones de no confusión
La 4ª asunción (no confusor M→Y afectado por X) es crítica
El paquete mediation implementa estos métodos
Siempre realizar análisis de sensibilidad

8.1 Objetivos de aprendizaje

8.2 ¿Qué es la mediación?

8.3 Definiciones causales

8.3.1 Efectos naturales (NDE y NIE)

8.4 Asunciones para identificación

8.5 Método de Baron-Kenny (tradicional)

8.5.1 Limitaciones del método tradicional

8.6 Método de mediación causal

8.6.1 Interpretación de resultados

8.7 Mediación con resultados binarios

8.8 Análisis de sensibilidad para mediación

8.9 Múltiples mediadores

8.10 Ejercicios

8.11 Resumen

Referencias